Решите уравнение
\(\log_2(4-x)=7\)
Найдите значение выражения
\(\dfrac{2^{4,4} \cdot 6^{7,4}}{12^{6,4}}\)
На рисунке изображён график функции 𝑦 = 𝑓′(𝑥) - производной функции 𝑓(𝑥), определенной на интервале (−5; 5). Найдите точку минимума функции 𝑓(𝑥).
В розетку электросети подключены приборы, общее сопротивление которых составляет \(R_{1}=90\) Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление \(R_{2}\) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями \(R_{1}\) Ом и \(R_{2}\) Ом их общее сопротивление дается формулой \(R_{\text {общ }}=\dfrac{R_{1} R_{2}}{R_{1}+R_{2}}\) (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше \(9\) Ом. Ответ выразите в омах.
Графики функций \(y=k x\) и \(y=a x^{2}+b x\) пересекаются в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).
Найдите точку минимума функции \(y=x \sqrt{x}-9 x+4\).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2};4\pi\right]\)
Точка \(D\) не лежит в плоскости равностороннего треугольника \(ABC\). При этом \(\cos(\angle DAB)=\cos(\angle DAC)=0,3\).
a) Докажите, что прямые \(AD\) и \(BC\) перпендикулярны.
б) Найдите расстояние между прямыми \(AD\) и \(BC\), если известно, что \(AB=6\).
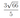
Решите неравенство
\(15\)-ого декабря планируется взять кредит в банке на сумму \(900\) тысячи рублей на \(13\) месяцев. Условия его возврата таковы:
- \(1\)-ого числа каждого месяца долг возрастает на \(3\%\) по сравнению с концом предыдущего
месяца;
- со \(2\)-го по \(14\)-е число каждого месяца необходимо выплатить часть долга;
- \(15\)-ого числа каждого месяца с \(1\)-го по \(12\)-й долг должен быть на на одну и ту же сумму меньше
долга на \(15\)-е число предыдущего месяца;
- к \(15\)-му числу \(13\)-го месяца кредит должен быть полностью погашен.
Какой долг будет \(15\)-го числа \(12\)-го месяца, если общая сумма выплат после полного
погашения кредита составит \(1134\) тысячи рублей?
В треугольник \(ABC\) вписана окружность, которая касается \(AB\) в точке \(P\). Точка \(М\) середина стороны \(AB\).
а) Докажите, что \(MP=\dfrac{|BC-AC|}{2}\).
б) Найдите углы треугольника \(ABC\), если известно, что отрезок \(MP\) равен половине радиуса окружности вписанной в треугольник \(ABC\), \(BC>AC\) и отрезки \(MC\) и \(MA\) равны.
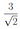
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет \(3\) различных решения.
Каждое из \(4\) последовательных натуральных чисел разделили на свою первую цифру. Пусть \(S\) сумма \(4\) получившихся чисел.
а) Может ли \(S=41\dfrac{11}{24}\)?
б) Может ли \(S=569 \dfrac{29}{72}\)?
в) Какое наибольшее целое значение может принимать \(S\), если известно, что \(4\) исходных числа не меньше \(400\) и не больше \(999\)?