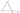
На координатной плоскости изображены векторы \(\vec{a}\) и \(\vec{b}\). Найдите скалярное произведение \(\vec{a}\cdot \vec{b}\).
Решите уравнение \(3^{1-x}=81\)
Найдите значение выражения \(\log_2{56}-\log_2{7}\).
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a\) км/ч\({}^2\). Скорость \(v\) вычисляется по формуле \(v = \sqrt {2la}\), где \(l\) - пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав \(0,8\) километра, приобрести скорость \(120\) км/ч. Ответ дайте в км/ч\({}^2\).
На рисунке изображён график функции \(f\left(x\right)=ax^{2} +bx+c\). Найдите \(f\left(10\right)\).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{9\pi}{2};-3\pi\right]\)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)
В правильной четырехугольной призме \(ABCDA_1B_1C_1D_1\) плоскость \(\alpha\) выходит из вершины \(B_1\) и \(D\), пересекает стороны \(AA_1\) и \(CC_1\) в точках \(M\) и \(K\) соответственно и является ромбом.
a) Докажите, что \(M -\) середина ребра \(AA_1\).
б) Найдите высоту призмы, если площадь основания равна \(3\), а площадь сечения равна \(6\).
В прямоугольном параллелепипеде \(ACBDA_1B_1C_1D_1\) известно, что \(AB =3, AD = 4, AA_1 = 6\).
Через точки \(B_1\) и \(D\) параллельно \(AC\) проведена плоскость, пересекающая ребро \(CC_1\) в точке \(K\).
а) Докажите, что \(K -\) середина \(CC_1\).
б) Найдите расстояние от точки \(B\) до плоскости сечения.
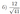
Решите неравенство
Решите неравенство
а) Докажите, что ∠𝐵𝐴𝐻 = ∠𝐵𝐵1𝐶1.
б) Найдите расстояние от центра описанной окружности до 𝐵𝐶, если 𝐶1𝐵1=18, а ∠𝐵𝐴𝐶 = 30∘.
Дан остроугольный треугольник \(ABC\). В нём высоты \(BB_1\) и \(CC_1\) пересекаются в точке \(H\).
а) Докажите, что \(\angle AHB_1=\angle ACB\).
б) Найдите \(BC\), если \(AH=8\sqrt{3}\) и \(\angle BAC=60^{\circ}\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет один корень на отрезке \([0;1]\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет один корень на отрезке \([0;1]\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет один корень на отрезке \([0;1]\).
а) Может ли сумма этих чисел быть равна 2205?
б) Может ли сумма этих чисел равна 3435?
в) Чему равна наибольшая возможная сумма этих чисел?