ЕГЭ 2025
досрочного
Площадь параллелограмма \(ABCD\) равна 70. Точка \(E\) - середина стороны \(AD\). Найдите площадь трапеции \(BCDE\).
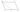
Даны векторы \(\vec{a}(5;2)\) и \(\vec{b}(3;-6)\). Найдите скалярное произведение вектора \(\vec{a}-\vec{b}\) и \(5\vec{a}-\vec{b}\).
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 2. Найдите площадь боковой поверхности призмы.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Труд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Труд» начнёт только последнюю игру.
Помещение освещается фонарём с тремя лампами. Вероятность перегорания каждой отдельной лампы в течение года равна 0,25. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. Результат округлите до тысячных.
Решите уравнение \(\log_{7}(4-x)=2\)
Найдите \(15\cos 2\alpha \), если \(\sin \alpha =0,6\).
На рисунке изображён график \(y = f'(x)\) — производной функции \(f(x)\). На оси абсцисс отмечено девять точек: \(x_1, x_2 ,x_3 ,x_4 ,x_5 ,x_6 ,x_7 ,x_8 ,x_9\). Сколько из этих точек принадлежит промежуткам убывания функции \(f(x)\)?
Мотоциклист, движущийся по городу со скоростью \(v_0=57\) км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением \(a=8\) км/ч\({}^2\). Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением \(S=v_0t+\frac{at^2}{2}\), где \(t\) - время в часах. Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 45 км от города. Ответ выразите в минутах.
Один мастер может выполнить заказ за 15 часов, а другой - за 10 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
На рисунке изображён график функции \(f\left(x\right)=a\sqrt{x}\) и \(g\left(x\right)=kx\), пересекающиеся в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).
Найдите точку минимума функции
\(y=(7x^2-21x-21)\cdot e^{x+12}\)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\pi;\dfrac{5\pi}{2}\right]\)
Дана правильная треугольная призма \(ABCA_1B_1C_1\). Точка \(M\,\, -\) середина ребра \(CC_1\). Через точки \(A_1\), \(M\) и \(B\) проведена плоскость \(\alpha\).
a) Докажите, что сечением призмы плоскостью \(\alpha\) является равнобедренный треугольник.
б) Найдите высоту призмы, если известно, что площадь сечения равна 6 и \(AB=2\).
Решите неравенство
Решите неравенство
Строительство нового завода стоит 159 млн рублей. Затраты на производство \(x\) тыс. ед. продукции на таком заводе равны \(0,5 x^2+2 x+6\) млн рублей в год. Если продукцию завода продать по цене \(p\) тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит \(p x-\left(0,5 x^2+2 x+6\right)\). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При этом в первый год \(p=10\), а далее каждый год возрастает на 1. За сколько лет окупится строительство?
Сумма оснований трапеции равна 17, а её диагонали равны 8 и 15.
a) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет более трёх различных решений.
Найдите все значения параметра \(a\), при каждом из которых уравнение
либо имеет единственное решение, либо не имеет решений.
В группе поровну юношей и девушек. Юноши отправляли электронные письма девушкам. Каждый юноша отправил или 4 письма, или 21 письмо, причём и тех и других юношей было не менее двух. Возможно, что какой-то юноша отправил какой-то девушке несколько писем.
a) Могло ли оказаться так, что каждая девушка получила ровно 7 писем?
б) Какое наименьшее количество девушек могло быть в группе, если известно, что все они получили писем поровну?
в) Пусть все девушки получили различное количество писем (возможно, какая-то девушка не получила писем вообще). Какое наибольшее количество девушек в такой группе?