ЕГЭ 2023

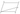


Найдите корень уравнения \(\left(\dfrac{1}{3}\right)^{(x-8)}=\dfrac{1}{9}\)
Найдите корень уравнения \(3^{x-2}=81\)
Найдите значение выражения \(\log_{\sqrt[6]{13}}13\).
Найдите значение выражения \(\log_{0,7}{10}-\log_{0,7}{7}\).

𝑥 = {𝑥1, 𝑥2, 𝑥3, ..., 𝑥𝑛}. Сколько из этих точек лежит на промежутках возрастания функции 𝑓(𝑥)?

К источнику с ЭДС \(\varepsilon = 55\) В и внутренним сопротивлением \(r = 0,5\) Ом, хотят подключить нагрузку с сопротивлением \(R\) Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даeтся формулой \(U = \frac{{\varepsilon R}}{{R + r}}\). При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 55 В? Ответ дайте в омах.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 598 МГц. Скорость погружения батискафа вычисляется по формуле \(v =c\cdot \dfrac{f-f_0}{f+f_0}\), где \(c=1500\) м/с - скорость звука в воде, \(f_0\) - частота испускаемых импульсов, \(f\) - частота отражённого от дна сигнала, регистрируемая приёмником (в МГц). Определите наибольшую возможную частоту отражённого сигнала \(f\), если скорость погружения батискафа не должна превышать 5 м/c. Ответ дайте в МГц.

На рисунке изображены графики функций \(f\left(x\right)=a\sqrt{x}\) и \(g\left(x\right)=kx+b\), которые пересекаются в точке \(A\). Найдите абсциссу точки \(A\).
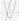
Найдите точку максимума функции \(y = -\dfrac{2}{3}x^{\frac{3}{2}}+3x+1\).
Найдите наименьшее значение функции \(y = 7+6x-2x\sqrt{x}\) на отрезке \([1;10]\).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2};4\pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-3\pi;-\dfrac{5\pi}{2}\right]\)

а) Докажите, что 𝑁 – середина 𝐵𝐶.
б) Найдите площадь трапеции 𝐴𝑀𝐾𝑁 , если объём призмы 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 равен 12, а ее высота равна 2
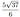
основаниями 𝐴𝐷 = 5 и 𝐵𝐶 = 4. 𝑀 – точка, которая делит сторону 𝐴1𝐷1 в отношении 1:4, 𝐾 – середина 𝐷𝐷1.
a) Доказать, что 𝑀𝐶𝐾||𝐵𝐷.
б) Найти тангенс угла между плоскостью 𝑀𝐾𝐶 и плоскостью основания, если ∠𝐵𝐴𝐷 = 60∘, а ∠𝐶𝐾𝑀 = 90∘.
а) Докажите, что прямая 𝐴𝐵 параллельна плоскости 𝛼.
б) Найдите отношение, в котором плоскость 𝛼 делит 𝑃𝑄, если 𝐴𝐴1 = 5, 𝐴𝐵 = 12, cos ∠𝐴𝐵𝐶 = 3/5.
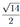
Решите неравенство
Решите неравенство
Решите неравенство
Решите неравенство
Решите неравенство

Решите неравенство
– в январе начисляется 𝑟% по кредиту.
с февраля по июнь в 2026, 2027, 2028, 2029, 2030 долг уменьшается равномерно на какую-то сумму.
– в конце 2030 года долг составляет 200 тыс. руб.
– с февраля по июнь в 2031, 2032, 2033, 2034, 2035 долг уменьшается равномерно на другую сумму.
– к 2035 году кредит должен быть выплачен.
Найдите 𝑟, если общая сумма выплат составила 1480 тыс. руб.
– каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
– с февраля по июнь в 2026, 2027, 2028, 2029, 2030 долг уменьшается равномерно на какую то сумму;
– с февраля по июнь в 2031, 2032, 2033, 2034, 2035 долг уменьшается равномерно на другую сумму;
– к 2035 году кредит должен быть выплачен.
Какая выплата была в 2026 году, если общая сумма выплат составила 1420 тыс. руб.
— каждый январь долг увеличивается на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого из годов с 2026 по 2030 долг уменьшается на одну и ту же сумму по сравнению с июлем предыдущего года;
— в июле каждого из годов с 2031 по 2035 долг уменьшается на одну и ту же сумму по сравнению с июлем предыдущего года, отличную от суммы, на которую долг убывал в первые пять лет.
Известно, что в конце 2030 года долг составил 800 тысяч рублей. Найдите начальную сумму кредита, если сумма выплат по кредиту равна 2090 тысяч рублей.
а) Доказать что угол 𝐴𝐸𝑀 равен углу 𝐶𝑀𝐾.
б) Найти отношение площадей треугольников 𝐴𝐸𝑀 и 𝐶𝑀𝐾, если 𝐴𝑀 :𝐶𝑀 = 1:4.
а) Докажите, что точки 𝑀 , 𝑁 и 𝑂 лежат на одной прямой.
б) Найдите 𝐴𝑀 : 𝑀𝐵, если известно, что 𝐴𝑂 = 𝑂𝐶 и 𝐵𝐶:𝐴𝐷 = 1:7.
а) Докажите, что cos ∠𝐵𝐴𝐷 = 0,2.
б) Найдите площадь ромба, если 𝑀𝑁 = 5.
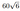
Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет ровно 2 различных решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет ровно 2 различных решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет ровно 2 различных решения.
Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет ровно 2 различных решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет ровно 2 различных решения.

a) Можно ли из дроби 2/3 получить дробь 29/41 .
б) Можно ли из некоторой дроби получить дробь 6/7 за 2 хода.
в) Дробь с/𝑑 больше 7/10 . Найдите минимальную дробь c/𝑑 , которую нельзя получить из другой правильной несокращаемой дроби за 2 хода.
а) Можно ли за 20 ходов создать пару, где одно из чисел равно 50?
б) За сколько ходов можно сделать пару, где сумма чисел будет равна 600?
в) Какое наибольшее число ходов можно сделать, чтобы оба числа не превышали 50?
а) Может ли в классе быть 9 девочек?
б) Может ли в классе быть 55% девочек, если придёт ещё одна?
в) Какова максимальная доля девочек, если в класс придёт одна девочка? (max. доля ∈ Z)
а) Можно ли получить число 200 за 100 ходов?
б) Сколько нужно сделать ходов, чтобы получить сумму равную 300
в) Сколько нужно сделать ходов, чтобы получить максимальную сумму, при этом ни одно число не превышает 200.
a) Существуют ли трёхзначные числа 𝐴 и 𝐵, для которых 𝑆 = 100?
б) Существуют ли пятизначные числа 𝐴 и 𝐵. для которых 𝑆 = 400?
в) Верно ли, что любое натуральное число от 1 до 260 является суммой для некоторых четырёхзначных чисел 𝐴 и 𝐵?
а) Может ли быть верным уравнение 𝐴 = 𝐵 · 𝐶, если 𝐴 > 140?
б) Может ли быть верным уравнение 𝐴 = 𝐵 · 𝐶, если 440 ⩽ 𝐴 < 500?
в) Найдите наибольшее число 𝐴 до 900, для которого выполняется 𝐴 = 𝐵 ·𝐶

⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ