ЕГЭ 2024

Даны векторы \(\vec{a}(1;1)\) и \(\vec{b}(0;7)\). Найдите длину вектора \(5\vec{a}+\vec{b}\).
Даны векторы \(\vec{a}(3;-2)\) и \(\vec{b}(0;1)\). Найдите длину вектора \(\vec{a}\cdot \vec{b}\).


Найдите корень уравнения \(\sqrt{2x+37}=7\)
Найдите корень уравнения \(\left(\dfrac{1}{2}\right)^{6-2x}=4\)
Найдите значение выражения \(2\sqrt{3}\cos^2{\dfrac{13\pi}{12}}-\sqrt{3}\).
Найдите значение выражения \(5\sqrt{2}\cos{\dfrac{3\pi}{8}}\sin{\dfrac{3\pi}{8}}\).


Автомобиль, движущийся в начальный момент времени со скоростью \(v_0 = 23\) м/с, начал торможение с постоянным ускорением \(a = 2\) м/с\(^2\). За \(t\) - секунд после начала торможения он прошёл путь \(S=v_0t-\dfrac{at^2}{2}\) (м).
Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 132 метра. Ответ дайте в секундах.
Для определения эффективной температуры звёзд используют закон Стефана-Больцмана, согласно которому \(P = \sigma ST^4 \), где \(P\) - мощность излучения звезды (в Ваттах), \(\sigma=5,7 \cdot 10^{-8} \frac{\text{Вт}}{\text{м}^2\cdot\text{К}^4}\) - постоянная, \(S\) - площадь поверхности звезды (в квадратных метрах), а \(T\) - температура (в Кельвинах). Известно, что площадь поверхности некоторой звезды равна \(\frac{1}{{729}} \cdot 10^{20} \text{м}^2\), а мощность её излучения равна \(5,13\cdot 10^{25}\) Вт. Найдите температуру этой звезды в Кельвинах.
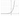

На рисунке изображён график функции \(f\left(x\right)=\dfrac{k}{x}\). Найдите \(f\left(10\right)\).
Найдите точку минимума функции \(y=5x-\ln{(x-7)}\)
Найдите точку минимума функции \(y=\dfrac{2}{3}x^{\frac{3}{2}}-2x+1\)
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[2\pi;\dfrac{7\pi}{2}\right]\)

а) Докажите, что точка 𝑀 – середина ребра 𝑆𝐶.
б) Найдите длину отрезка, по которому плоскость 𝑂𝑀𝑁 пересекает грань 𝑆𝐵𝐶.
а) Докажите, что прямые 𝐿𝐾, 𝑀𝑁 и 𝐵𝑆 пересекаются в одной точке.
б) Найдите отношение 𝐶𝑁:𝑁𝐵.
а) Докажите, что прямая 𝑀𝑁 перпендикулярна ребрам 𝐴𝐵 и 𝐶𝐷.
б) Найдите площадь сечения тетраэдра 𝐴𝐵𝐶𝐷 плоскостью 𝛼, если известно,
что 𝐵𝐾 = 1, 𝐾𝐶 = 5.
Решите неравенство
Решите неравенство

Решите неравенство
Решите неравенство
Решите неравенство
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года.
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долго.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен четырьмя равными платежами (т.е. за 4 года) и общая сумма платежей составит 375000 рублей.
- каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года.
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долго.
Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (т.е. за 3 года) и общая сумма выплат после полного погашения кредита на 65500 рублей больше
суммы, взятой в кредит?
- каждый январь долг возрастает на 25% по сравнению с концом предыдущего года.
- в июле 2027, 2028, 2029 годов долг остается равным 720 тыс. руб.
- выплаты в 2030 и 2031 годах равны.
- к июлю 2031 года долг будет выплачен полностью.
Найдите общую сумму платежей за пять лет.
а) Докажите, что стороны пятиугольника равны.
б) Найдите 𝐴𝐵, если известно, что 𝐵𝐸 = 12, 𝐵𝐶 = 5, 𝐴𝐷 = 9.
а) Докажите, что 𝐴𝐶 = 𝐶𝐸.
б) Найдите 𝐵𝐸, если известно, что 𝐴𝐷 = 10.
а) Докажите, что прямая 𝐴𝐶 параллельна биссектрисе угла 𝐴𝑁𝐵.
б) Найдите 𝑁𝑂, если 𝐴𝐵 = 24, 𝐴𝐶 = 10.
а) Докажите, что 𝐴𝐶 = 6.
б) Найдите площадь треугольника 𝐴𝐵𝐶, если ∠𝐴𝐶𝐵 = 90∘.
Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет 2 решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет 2 решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет 2 решения.
Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет 4 решения.

Найдите все значения параметра \(a\), при каждом из которых система уравнений
имеет 1 решение.

а) Может ли масса контейнеров с сахарным песком составить 50% от общей массы всех контейнеров?
б) Может ли масса контейнеров с сахарным песком составить 60% от общей массы всех контейнеров?
в) Какую наименьшую долю(в процентах) может составить масса контейнеров с сахарным песком от общей массы всех контейнеров?
a) Может ли разность масс двух этих кучек камней быть равна 6 кг?
б) Могут ли массы двух этих кучек быть равны?
в) Какая наименьшая положительная разность масс может быть у двух этих кучек камней?
а) можно ли получить 175?
б) можно ли получить 176?
в) сколько нужно добавить монет по 1 рублю, чтобы можно было собрать любую сумму от 1 до 180 включительно?
а) Возможно ли из какой-то пары получить пару (5; 5)?
б) Верно ли, что если пара (𝑐; 𝑑) может быть получена из какой-то пары с помощью данной операции, то и пара (−𝑑; с) тоже может быть получена из какой-то пары с помощью данной операции?
в) Зададим расстояние между парами целых чисел (а; 𝑏) и (𝑐; 𝑑) выражением |𝑎 − 𝑐| + |𝑏 − 𝑑|. Найдите наименьшее расстояние от пары (9; 2) до пары, полученной из какой-то пары с помощью данной операции.

⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ