вариант

В треугольнике \(ABC\) стороны \(AC\) и \(BC\) равны. Внешний угол при вершине \(B\) равен \(149^\circ\). Найдите угол \(C\). Ответ дайте в градусах.

Острый угол \(B\) прямоугольного треугольника \(ABC\) равен \(48^\circ\). Найдите угол между высотой \(CH\) и биссектрисой \(CD\), проведёнными из вершины прямого угла. Ответ дайте в градусах.

В треугольнике \(ABC\) угол \(C\) равен \(50^\circ\), \(AD\) - биссектриса, угол \(BAD\) равен \(54^\circ\). Найдите угол \(ADB\). Ответ дайте в градусах.

Наблюдатель находится на высоте \(h\), выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле \(l = \sqrt {\frac{Rh}{500}}\), где \(R = 6400\) км - радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии \(172\) километров? Ответ дайте в метрах.

Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением \(a\) км/ч\({}^2\). Скорость \(v\) вычисляется по формуле \(v = \sqrt {2la}\), где \(l\) - пройденный автомобилем путь. Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав \(0,3\) километра, приобрести скорость \(90\) км/ч. Ответ дайте в км/ч\({}^2\).

Теплоход проходит по течению реки до пункта назначения \(425\) км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна \(4\) км/ч, стоянка длится \(8\) часов, а в пункт отправления теплоход возвращается через \(50\) часов после отплытия из него. Ответ дайте в км/ч.

На рисунке изображены графики функций \(f\left(x\right)=\dfrac{k}{x} \) и \(g\left(x\right)=ax+b\), которые пересекаются в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).

На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

На рисунке изображены графики функций \(f\left(x\right)=ax^2+bx+c\) и \(g\left(x\right)=kx\), которые пересекаются в точках \(A\) и \(B\). Найдите абсциссу точки \(B\).

Найдите точку максимума функции \(y=x^3 -12x^2+36x+87\).

а) Решите уравнение

а) Решите уравнение

В правильной четырёхугольной пирамиде \(SABCD\) с основанием \(ABCD\), сечение \(\alpha\) проходит через \(AB\) и пересекает \(SC\) и \(SD\) в точках \(N\) и \(M\), \(AB=AM=BN=5MN\).

a) Докажите, что \(SN:NC=1:4\).

б) Найдите тангенс угла между плоскостью \(\alpha\) и основанием пирамиды.

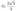
В правильной четырёхугольной пирамиде \(SABCD\) с основанием \(ABCD\), сечение \(\alpha\) проходит через \(AB\) и пересекает \(SC\) и \(SD\) в точках \(N\) и \(M\), \(AB=AM=BN=5MN\).

a) Докажите, что \(SN:NC=1:4\).

б) Найдите тангенс угла между плоскостью \(\alpha\) и основанием пирамиды.

В правильной треугольной призме \(A B C A_1 B_1 C_1\) отметили точки \(M\) и \(K\) на ребрах \(A A_1\) и \(A_1 B_1\) соответственно. Известно, что \(A_1 M=2 A M, A_1 K=K B_1\). Через точки \(M\) и \(K\) провели плоскость \(\alpha\) перпендикулярно грани \(A B B_1 A_1\).

a) Докажите, что плоскость \(\alpha\) проходит через вершину \(C_1\).

б) Найдите площадь сечения призмы \(A B C A_1 B_1 C_1\) плоскостью \(\alpha\), если все ребра призмы равны \(20\).

В правильном тетраэдре \(ABCD\). На \(AB, BC\) и \(AD\) отмечены точки \(M,\,\, L\) и \(N\) соответственно так, что \(AM:MB=BL:LC=AN:ND=1:4\).

a) Докажите, что плоскость \(\alpha\), проходящая через точки \(L,\,\, M,\,\, N\), делит ребро \(CD\) в отношении \(4:1\), считая от вершины \(C\).

б) Найдите площадь сечения тетраэдра \(ABCD\) плоскостью \(\alpha\), если \(AB=10\).

Плоскость \(\alpha\) перпендикулярна плоскости основания \(ABCD\) правильной четырёхугольной пирамиде \(SABCD\) и пересекает сторону \(SA\) в точке \(K\). Сечение - правильный треугольник площадью \(2\sqrt{3}\).

a) Докажите, что плоскость \(\alpha\) перпендикулярна \(AC\).

б) Найдите, в каком отношении точка \(K\) делит сторону \(SA\), если объём \(SABCD\) равен \(36\sqrt{6}\) см\(^3\).

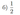
Решите неравенство

Решите неравенство

Решите неравенство

\(15\) декабря \(2026\) года планируется взять кредит в банке на сумму \(18\) млн рублей на \(36\) месяцев. Условия его возврата таковы:

— \(1\)-го числа каждого месяца долг возрастает на \(r\%\) по сравнению с концом предыдущего месяца;

— со \(2\)-го по \(14\)-е число каждого месяца необходимо одним платежом оплатить часть долга;

— \(15\)-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на \(15\)-е число предыдущего месяца;

— к \(15\) декабря \(2029\) года кредит должен быть полностью погашен.

Чему равно \(r\), если общая сумма платежей в \(2027\) году составляет \(7830\) тыс.рублей?

\(15\) декабря \(2026\) года планируется взять кредит в банке на сумму \(6\) млн рублей на \(24\) месяца. Условия его возврата таковы:

— \(1\)-го числа каждого месяца долг возрастает на \(3 \%\) по сравнению с концом предыдущего месяца;

— со \(2\)-го по \(14\)-е число каждого месяца необходимо одним платежом оплатить часть долга;

— \(15\)-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на \(15\)-е число предыдущего месяца;

— к \(15\) декабря \(2028\) года кредит должен быть полностью погашен.

Чему равна общая сумма платежей в \(2027\) году?

В июле планируется взять кредит в банке на сумму \(14\) млн рублей на некоторое целое число лет. Условия его возврата таковы:

— каждый январь долг возрастает на \(25\%\) по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплачивать часть долга;

— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.

На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась \(24,5\) млн рублей?

\(15\) декабря \(2026\) года взяли кредит в размере \(A\) млн. рублей на срок \(48\) месяцев. Условия выплаты кредита таковы:

— \(1\)-ого числа каждого месяца на оставшуюся сумму долга начисляются проценты в размере \(1\%\) от оставшейся суммы долга.

— с \(1\)-ого по \(15\)-ое число каждого месяца должна быть произведена выплата.

— Каждый следующий месяц долг должен быть на одну и ту же величину меньше

— к \(2030\) году долг должен быть выплачен полностью.

В каком размере был взят кредит в \(A\) млн. рублей, если известно, что общая сумма платежей за \(2030\) год составила \(6390\) тыс. рублей?

В треугольнике \(A B C\) проведены высота \(A H\) и медиана \(A M\), угол \(A C B\) равен \(30^{\circ}\). Точка \(H\) лежит на отрезке \(B M\). В треугольнике \(A C M\) проведена высота \(M Q\). Прямые \(M Q\) и \(A H\) пересекаются в точке \(F\). Известно, что \(A M\) - биссектриса угла \(H A C\).

a) Докажите, что треугольник \(A B C\) прямоугольный.

б) Найдите площадь треугольника \(C F M\), если \(A B=10\).

В четырёхугольнике \(KLMN\) вписана окружность с центром в точке \(O\). Эта окружность касается стороны \(MN\) в точке \(A\), \(\angle MNK=90^{\circ}\), \(\angle KLM=\angle LMN=60^{\circ}\).

a) Докажите что точка \(A\) лежит на прямой \(LO\).

б) Найдите \(MN\), если \(LA=3\sqrt{3}\).

В четырёхугольнике \(KLMN\) вписана окружность с центром в точке \(O\). Эта окружность касается стороны \(MN\) в точке \(A\), \(\angle N=90^{\circ},\,\, \angle K=\angle L=120^{\circ}\).

a) Докажите что точка \(O\) лежит на прямой \(LA\).

б) Найдите \(MN\), если \(LA=3\).

Дан остроугольный треугольник \(A B C\). Известно, что \(\angle B A C=2 \angle A B C\). Точка \(O\) - центр описанной окружности треугольника \(A B C\). Вокруг треугольника \(A O C\) описана окружность, которая пересекает сторону \(B C\) в точке \(P\).

a) Докажите, что треугольники \(A B C\) и \(P A C\) подобны.

б) Найдите \(A B\), если \(B C=\sqrt{21}\) и \(A C=3\).

Дан параллелограмм \(ABCD\) угол \(BAD\) - острый. Проведены высоты \(BP\) и \(BQ\), точка \(P\) лежит на стороне \(AD\), а точка \(Q\) - на стороне \(CD\). На \(AD\) отмечена точка \(M\). Известно, что \(BP=AM\) и \(AB=BQ\).

a) Докажите, что \(BM=PQ\).

б) Найдите площадь треугольника \(APQ\), если \(BP=AM=8,\,\, AB=BQ=10\).

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Найдите все значения параметра \(a\), при каждом из которых уравнение

Записаны \(10\) различных натуральных чисел. Известно, что среднее арифметическое любых четырёх или семи из них – целое число.

a) Могут ли быть среди записанных чисел \(563\) и \(1417\)?

б) Может ли одно из написанных на доске чисел быть квадратом натурального числа, если на доске есть число \(563\)?

в) Пусть среди записанных чисел есть \(1\) и \(n^2\), где \(n\) – натуральное число, большее единицы. Найдите наименьшее возможное \(n\).

На доске записано \(k\) последовательных натуральных чисел. Оказалось, что среди них чисел, делящихся на \(20\), меньше, чем чисел, делящихся на \(23\).

a) Могло ли среди записанных чисел быть ровно три числа, делящихся на \(20\)?

б) Могло ли среди записанных чисел быть ровно десять чисел, делящихся на \(20\)?

в) Найдите наибольшее возможное значение \(k\).

На доске написано \(10\) различных натуральных чисел. Известно, что среднее арифметическое любых трех, четырех, пяти или шести чисел является целым числом. Одно из записанных чисел равно \(30032\).

a) Может ли среди написанных на доске чисел быть число \(312\)?

б) Может ли отношение двух записанных на доске чисел быть равным \(6\)?

в) Отношение двух написанных на доске чисел является целым числом \(n\). Найдите наименьшее возможное значение \(n\).