25.03.2025
Один из углов треугольника равен \(40^{\circ}\), а величины двух других относятся как \(2: 3\). Найдите больший угол этого треугольника. Ответ дайте в градусах.
Длина вектора \(\vec{a}\) равна \(5 \sqrt{3}\), угол между векторами \(\vec{a}\) и \(\vec{b}\) равен \(60^{\circ}\), а скалярное произведение векторов \(\vec{a}\) и \(\vec{b}\) равно \(11 \sqrt{3}\). Найдите длину вектора \(\vec{b}\).
Боковые рёбра треугольной пирамиды взаимно перпендикулярны, длина каждого из них равна 6. Найдите объём пирамиды.
В пенале у Полины лежали фишки с номерами от 1 до 22. Брат Юра потерял две фишки с чётными номерами. Найдите вероятность того, что случайно взятая Полиной фишка окажется с чётным номером.
Рекламное агентство использует автоматическую телефонную станцию, которая по введённому списку телефонных номсров дозванивается до абонентов и при ответе передаёт записанное голосовое сообщсние. При отсутствии ответа станция набирает номер ещё раз. Если с абонентом не удалось соединиться после пяти попыток, станция набирает номер другого абонента. Установлено, что станция может дозвониться до абонента с первого раза с вероятностью 0,3, а при каждом следующем наборе номера этого абонента вероятность увеличивается на 0,1. Найдите вероятность того, что станция сможет передать абоненту сообщение не позднее третьего набора его номера.
Найдите корень уравнения \(\sqrt{2 x}+\sqrt{3}=\sqrt{27}\).
Найдите значение выражения \(\log _2 3 \cdot \log _9 2\).
На рисунке изображён график \(y=f^{\prime}(x)\) - производной функции \(f(x)\), определённой на интервале \((-3 ; 9)\). Найдите количество точек минимума функции \(f(x)\), принадлежащих отрезку \([-2 ; 8,5]\).
После дождя уровень воды в колодце повышастся. Мальчик измеряет время падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле \(h=5 t^2\), где \(h\) - расстояние (в метрах), \(t\) - время падения (в секундах). До дождя время падения камешков составляло 0,6 секунды. На сколько метров должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 секунды? Ответ дайте в метрах.
Имеется два сплава. Первый сплав содержит \(10 \%\) меди, второй - \(40 \%\) меди. Масса второго сплава больше массы первого на \(3\) кг. Из этих двух сплавов получили третий сплав, содержащий \(30 \%\) меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
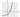
На рисунке изображён график функции \(f(x)=a^x+b\). Найдите значение \(x\), при котором \(f(x)=29\).
Найдите наибольшее значение функции \(y=x^3-147 x+11\) на отрезке \([-8 ; 0]\).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\pi ; \frac{\pi}{2}\right]\)
Сторона основания правильной треугольной призмы \(A B C A_1 B_1 C_1\) равна 12, а её боковое ребро равно 6. Плоскость сечения \(\alpha\) содержит ребро \(B C\) и пересекает луч \(A A_1\) в точке \(L\). Угол, образованный плоскостями \(\alpha\) и \(A B C\), равен \(60^{\circ}\).
a) Докажите, что сечение призмы \(A B C A_1 B_1 C_1\) плоскостью \(\alpha\) - трапеция.
б) Найдите площадь сечения призмы \(A B C A_1 B_1 C_1\) плоскостью \(\alpha\).
Решите неравенство
В июле 2025 года планируется взять кредит в банке на некоторую сумму на три года. Условия его возврата таковы:
- каждый январь долг увеличивается на \(20 \%\) по сравнению с концом предыдущего года;
- с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами и общая сумма платежей после полного погашения кредита должна быть на \(57900\) рублей больше суммы, взятой в кредит?
В равностороннем треугольнике \(A B C\) на стороне \(A B\) отмечена её середина - точка \(K\), на стороне \(B C\) отмечена её середина - точка \(M\). На отрезке \(K M\) отмечена точка \(E\) так, что \(K E: E M=1: 2\). Прямая \(A E\) пересекает сторону \(B C\) в точке \(N\).
a) Докажите, что прямая, проходящая через точку \(K\) параллельно прямой \(A N\), пересекает отрезок \(B N\) в его середине.
б) Найдите длину отрезка \(A N\), если \(A C=\sqrt{13}\).
Найдите все значения параметра \(a\), при каждом из которых фукнция
является нечётной.
Четверо одноклассников играют в числа. Первый записал несколько необязательно различных двузначных чисел. Второй нашёл их сумму, и у него получилось 231. Третий поменял местами единицы и десятки в каждом числе, записанном первым. Четвёртый нашёл сумму чисел, получившихся у третьего.
a) Может ли сумма чисел, найденная четвёртым, быть в 4 раза больше суммы, которую получил второй?
б) Может ли сумма чисел, найденная чствёртым, быть в 3 раза больше суммы, которую получил второй?
в) Какую наибольшую сумму может получить четвёртый?