ЕГЭ 2025
Четырехугольник \(A B C D\) вписан в окружность. Угол \(A B D\) равен \(75^{\circ}\), угол \(C A D\) равен \(35^{\circ}\). Найдите угол \(A B C\). Ответ дайте в градусах.
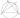
Отрезки \(AC\) и \(BD\) - диаметры окружности с центром \(O\). Угол \(ACB\) равен \(38^\circ\). Найдите угол \(AOD\). Ответ дайте в градусах.
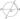
Даны векторы \(\vec{a}(-1 ; 4)\) и \(\vec{b}(2 ; 5)\). Найдите скалярное произведение векторов \(\vec{a}\) и \(\vec{b}\).
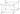
Найдите объем многогранника, вершинами которого являются точки \(A, B, C, D_{1}\) прямоугольного параллелепипеда \(A B C D A_{1} B_{1} C_{1} D_{1}\), у которого \(A B=3, A D=3, A A_{1}=4\).
Вероятность того, что на тестировании по истории учащийся Т. решит больше \(10\) задач, равна \(0,75\). Вероятность того, что Т. верно решит больше \(9\) задач, равна \(0,8\). Найдите вероятность того, что Т. верно решит ровно \(10\) задач.
В коробке 11 синих, 6 красных и 8 зелёных фломастеров. Случайным образом выбирают два фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастеры?
Решите уравнение \((7-4 x)^{2}=(2 x+5)^{2}\).
Если корней несколько, в ответе укажите наибольший корень.
Решите уравнение \(\sqrt{3-2 x}=2 x+3\).
Если уравнение имеет больше одного корня, в ответе запишите меньший из корней.
Найдите значение выражения \(\dfrac{(3 \sqrt{13})^{2}}{26}\).

На рисунке изображён график \(y=f^{\prime}(x)\) - производной функции \(f(x)\), определенной на интервале \((-9 ; 4)\). Найдите точку минимума функции \(f(x)\).
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением \(p_{1} V_{1}^{1,4}=p_{2} V_{2}^{1,4}\), где \(p_{1}\) и \(p_{2}\) - давление газа (в атмосферах) в начальном и конечном состояниях, \(V_{1}\) и \(V_{2}\) - объём газа (в литрах) в начальном и конечном состояниях. Изначально объём газа равен \(192\) л, а давление газа равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде стало \(128\) атмосфер? Ответ дайте в литрах.
Водолазный колокол, содержащий \(\nu=13\) молей воздуха при давлении \(p_{1}=1,2\) атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления \(p_{2}\). Работа, совершаемая водой при сжатии воздуха, определяется выражением \(A=\alpha \nu T \log _{2} \frac{p_{2}}{p_{1}}\), где \(\alpha=15 \frac{\text { Дж }}{\text { моль } \cdot K}-\) постоянная, \(T=300 K-\) температура воздуха. Найдите, какое давление \(p_{2}\) (в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в \(117000\) Дж.
Имеется два сосуда. Первый содержит \(30\) кг, а второй - \(20\) кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий \(68 \%\) кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий \(70 \%\) кислоты. Сколько килограммов кислоты содержится в первом сосуде?
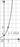
На рисунке изображён график функции вида \(f(x)=a^{x}\). Найдите значение \(f(3)\).
Найдите точку максимума функции \(y=\dfrac{196}{x}+x+7\).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{\pi}{2}; \pi\right]\)

а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2}; 4\pi\right]\)

Дан куб \(A B C D A_{1} B_{1} C_{1} D_{1}\). Точки \(M\) и \(K\) - середины его ребер \(A B\) и \(B C\) соответственно. Плоскость \(\alpha\) проходит через точку \(B\) параллельно прямым \(A_{1} M\) и \(B_{1} K\).
a) Докажите, что плоскость \(\alpha\) проходит через точку \(D\).
б) Найдите площадь сечения куба плоскостью \(\alpha\), если его ребра равны \(2\).
Дана правильная четырёхугольная призма \(A B C D A_{1} B_{1} C_{1} D_{1}\). Точка \(L\) лежит на стороне \(CC_1\), \(M\) - середина \(A_1B_1\). Точка \(K\) делит \(DC\) таким образом, что \(DK=2KC\). \(AKLM\) - равнобедренная трапеция.
a) Докажите, что \(CL=2C_1L\).
б) Найдите объём призмы, если известно, что \(AA_1=7\).
В прямоугольном параллелепипеде \(A B C D A_{1} B_{1} C_{1} D_{1}\) точка \(N\) - лежит на ребре \(CD\). Известно, что \(CN=2ND,\,\, AB=3AA_1,\,\, AD=2AA_1\).
a) Докажите, что плоскость \(\alpha\), проходящая через точки \(A,\,\, C_1,\,\, N\), делит ребро \(A_1B_1\) в отношении \(2:1\).
б) Найдите площадь сечения плоскостью \(\alpha\), если известно, что \(AA_1=1\).
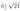
Решите неравенство
Решите неравенство
В июле планируется открыть вклад в банке под \(25 \%\) годовых на некоторую сумму. В начале второго, третьего и четвёртого годов со вклада снимают одну и ту же сумму. Найдите исходную сумму вклада, если после третьего снятия на вкладе осталось 0 рублей, а всего было снято \(375000\) рублей.
Вклад в размере \(10\) млн руб. планируется открыть на четыре года. В конце каждого года банк увеличивает размер вклада на \(10\%\). Кроме того в начале третьего и четвёртого годов вкладчик ежегодно пополняет вклад на \(x\) млн руб., где \(x\) — целое число. Найдите наименьшее значение \(x\), при котором банк за четыре года начислит на вклад больше \(7\) млн руб.
Петя \(1\) июля \(2026\) года положил на счёт в банке некоторую сумму (на накопительный счёт).
- \(30\) июня каждого года банк будет начислять \(25 \%\) на сумму, которая была \(29\) июня.
- \(1\) июля \(2027, 2028, 2029\) годов Петя будет снимать со счёта \(312500\) рублей.
- \(1\) июля \(2029\) года на счёте не останется денег.
Сколько должен положить Петя на счёт в банке в \(2026\) году?
Дан прямоугольник \(A B C D\). Известно, что \(C D=3 A D\). Точка \(M\) - середина его стороны \(A D\). На стороне \(C D\) отмечена точка \(N\). Известно, что \(C N=2 N D\). Точка \(K\) - середина отрезка \(C M\).
a) Докажите, что точки \(B, N\) и \(K\) лежат на одной прямой.
б) Найдите длину \(KN\), если известно, что \(AD=4\).
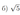
Дан треугольник \(ABC\). Биссектриса угла \(A\) пересекает \(BC\) в точке \(K\), а описанную около треугольника окружность - в точке \(M\).
a) Докажите, треугольник \(BCM\) - равнобедренный.
б) Найдите радиус описанной окружности около треугольника \(KCM\), если \(AB=8,\,\, BC=7,\,\, AC=6\).
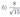
Дан треугольник \(ABC\). Биссектриса угла \(A\) пересекает \(BC\) в точке \(K\), а описанную около треугольника окружность - в точке \(M\).
a) Докажите, что биссектриса угла \(C\) делит отрезок \(M N\) пополам.
б) Пусть \(P\) - точка пересечения биссектрис треугольника \(A B C\). Найдите отношение \(A P: P N\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет ровно один корень на отрезке \([0 ; 1]\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет ровно один корень на отрезке \([0 ; 1]\).
Найдите все значения параметра \(a\), при каждом из которых уравнение
имеет ровно один корень на отрезке \([0 ; 1]\).
На доске написано \(20\) натуральных необязательно различных чисел, каждое из которых не превосходит \(50\). Одно или несколько из чисел на доске увеличили на \(1\). Числа, которые после этого оказались равны \(51\), с доски стёрли.
a) Могло ли среднее арифметическое всех чисел на доске уменьшиться?
б) Могло ли быть так, что сначала среднее арифметическое было равно \(24\), а потом стало равно \(17\)?
в) Чему может быть равно наименьшее среднее арифметическое чисел, оставшихся на доске, если изначально оно было равно \(24\)?
На доске написано \(20\) натуральных необязательно различных чисел, больших \(5\), каждое из которых не превосходит \(45\). После чего все числа на доске уменьшили на \(1\). Числа, которые после этого оказались равны \(5\), с доски стёрли.
a) Могло ли среднее арифметическое всех оставшихся на доске чисел увеличиться?
б) Могло ли быть так, что сначала среднее арифметическое было равно \(32\), а потом стало равно \(39\)?
в) Чему может быть равно наибольшее среднее арифметическое чисел, оставшихся на доске, если изначально оно было равно \(32\)?
На доске написаны \(30\) натуральных не обязательно различных чисел. Все они больше \(16\), но превосходят \(56\), а их среднее арифметическое равно \(23\). Все числа заменили на в два раза меньшие и после этого стерли те, что оказались меньше \(9\). При этом на доске обязательно осталось хотя бы одно число.
a) Может ли среднее арифметическое всех оставшихся чисел быть больше \(21\)?
б) Может ли среднее арифметическое всех чисел быть больше \(20\), но меньше \(21\)?
в) Какое наибольшее среднее арифметическое могло получиться у оставшихся чисел.

⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ