Планиметрия

Четырёхугольник \(ABCD\) вписан в окружность радиуса \(R=8\). Известно, что \(AB=BC=CD=12\).

а) Докажите, что прямые \(BC\) и \(AD\) параллельны.

б) Найдите \(AD\).

На стороне \(BC\) параллелограмма \(ABCD\) выбрана точка \(M\) такая, что \(AM=MC\).

а) Докажите, что центр вписанной в треугольник \(AMD\) окружности лежит на диагонали \(AC\).

б) Найдите радиус вписанной в треугольник \(AMD\) окружности, если \(AB=5, BC=10, \angle BAD=60^{\circ}\).

Окружность с центром в точке \(O\) высекает на всех сторонах трапеции \(ABCD\) равные хорды.

а) Докажите, что биссектрисы всех углов трапеции пересекаются в одной точке.

б) Найдите высоту трапеции, если окружность пересекает боковую сторону \(AB\) в точках \(K\) и \(L\) так, что \(AK=15, KL=6, LB=5\).

Окружность с центром в точке \(O\) касается сторон угла с вершиной \(N\) в точках \(A\) и \(B\). Отрезок \(BC\) — диаметр этой окружности.

а) Докажите, что прямая \(AC\) параллельна биссектрисе угла \(ANB\).

б) Найдите длину отрезка \(NO\), если известно, что \(AC=10\) и \(AB=24\).

Окружность с центром в точке \(O\) касается сторон угла с вершиной \(N\) в точках \(A\) и \(B\). Отрезок \(BC\) — диаметр этой окружности.

а) Докажите, что \(\angle ANB=2\angle ABC\).

б) Найдите расстояние от точки \(N\) до прямой \(AB\), если известно, что \(AC=14\) и \(AB=36\).

В треугольнике \(ABC\) продолжения высоты \(CC_1\) и биссектрисы \(BB_1\) пересекают описанную окружность в точках \(N\) и \(M\) соответственно, \(\angle ABC=40^{\circ}, \angle ACB=85^{\circ}\).

а) Докажите, что \(BM=CN\).

б) Прямые \(BC\) и \(MN\) пересекаются в точке \(D\). Найдите площадь треугольника \(BDN\), если его высота \(BH\) равна 6.

На стороне \(AC\) равностороннего треугольника \(ABC\) отмечена точка \(M\). Серединный перпендикуляр к отрезку \(BM\) пересекает стороны \(AB\) и \(BC\) в точках \(E\) и \(K\) соответственно.

а) Докажите, что треугольники \(AEM\) и \(CMK\) подобны.

б) Найдите отношение \(AM:MC\), если площади треугольников \(AEM\) и \(CMK\) равны 4 и 9 соответственно.

На стороне \(AC\) равностороннего треугольника \(ABC\) отмечена точка \(M\). Серединный перпендикуляр к отрезку \(BM\) пересекает стороны \(AB\) и \(BC\) в точках \(E\) и \(K\) соответственно.

а) Докажите, что \(\angle AEM=\angle CMK\).

б) Найдите отношение площадей треугольников \(AEM\) и \(CMK\), если \(AM:MC=1:4\).

Биссектрисы углов \(BAD\) и \(BCD\) равнобедренной трапеции \(ABCD\) пересекаются в точке \(O\). На боковых сторонах \(AB\) и \(CD\) отмечены точки \(M\) и \(N\) соответственно так, что \(AM=MO, CN=NO\).

а) Докажите, что точки \(M, O\) и \(N\) лежат на одной прямой.

б) Найдите отношение \(AM:MB\), если \(AO=CO\) и \(BC:AD=17:31\).

Биссектрисы углов \(BAD\) и \(BCD\) равнобедренной трапеции \(ABCD\) пересекаются в точке \(O\). Через точку \(O\) провели прямую, параллельную основаниям \(BC\) и \(AD\).

а) Докажите, что отрезок этой прямой внутри трапеции равен её боковой стороне.

б) Найдите отношение длин оснований трапеции, если \(AO=CO\) и данная прямая делит сторону \(AB\) в отношении \(AM:MB=1:2\).

В треугольнике \(ABC\) точки \(M\) и \(N\) лежат на сторонах \(AB\) и \(BC\) соответственно так, что \(AM:MB=CN:NB=2:3\). Окружность, вписанная в треугольник \(ABC\), касается отрезка \(MN\) в точке \(L\).

а) Докажите, что \(AB+BC=4AC\).

б) Найдите радиус окружности, вписанной в треугольник \(ABC\), если \(ML=\frac{9}{5}, LN=3\).

В параллелограмме \(ABCD\) угол \(BAC\) вдвое больше угла \(CAD\). Биссектриса угла \(BAC\) пересекает отрезок \(BC\) в точке \(L\). На продолжении стороны \(CD\) за точку \(D\) выбрана такая точка \(E\), что \(AE=CE\).

а) Докажите, что \(AL \cdot BC=AB \cdot AC\).

б) Найдите \(EL\), если \(AC=8, \operatorname{tg} \angle BCA=\frac{1}{2}\).

Прямая, перпендикулярная стороне \(BC\) ромба \(ABCD\), пересекает его диагональ \(AC\) в точке \(M\), а диагональ \(BD\) в точке \(N\), причём \(AM:MC=1:2, BN:ND=1:3\).

а) Докажите, что \(\cos \angle BAD=\frac{1}{5}\).

б) Найдите площадь ромба, если \(MN=5\).

Прямая, перпендикулярная стороне \(BC\) ромба \(ABCD\), пересекает его диагональ \(AC\) в точке \(M\), а диагональ \(BD\) в точке \(N\), причём \(AM:MC=1:2, BN:ND=1:3\).

а) Докажите, что прямая \(MN\) делит сторону ромба \(BC\) в отношении \(1:4\).

б) Найдите сторону ромба, если \(MN=\sqrt{6}\).

В квадрате \(ABCD\) точки \(M\) и \(N\) — середины сторон \(AB\) и \(BC\) соответственно. Отрезки \(CM\) и \(DN\) пересекаются в точке \(K\).

а) Докажите, что \(\angle BKM=45^{\circ}\).

б) Найдите радиус окружности, описанной около треугольника \(ABK\), если сторона \(AB=2\sqrt{10}\).

В остроугольном треугольнике \(ABC\) высоты \(AA_1, BB_1\) и \(CC_1\) пересекаются в точке \(H\). Через точку \(C_1\) параллельно высоте \(BB_1\) проведена прямая, пересекающая высоту \(AA_1\) в точке \(K\).

а) Докажите, что \(AB \cdot KH=BC \cdot C_1H\).

б) Найдите отношение площадей треугольников \(C_1HK\) и \(ABC\), если \(AB=6, BC=4, AC=5\).

На стороне \(BC\) треугольника \(ABC\) отмечена точка \(D\) так, что \(AB=BD\). Биссектриса \(BF\) треугольника \(ABC\) пересекает прямую \(AD\) в точке \(E\). Из точки \(C\) на прямую \(AD\) опущен перпендикуляр \(CK\).

а) Докажите, что \(AB:BC=AE:EK\).

б) Найдите отношение площади треугольника \(ABE\) к площади четырёхугольника \(CDEF\), если \(BD:DC=5:2\).

Окружность с центром \(O_1\) касается оснований \(BC\) и \(AD\) и боковой стороны \(AB\) трапеции \(ABCD\). Окружность с центром \(O_2\) касается сторон \(BC, CD\) и \(AD\). Известно, что \(AB=10, BC=9, CD=30, AD=39\).

а) Докажите, что прямая \(O_1O_2\) параллельна основаниям трапеции \(ABCD\).

б) Найдите \(O_1O_2\).

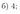
Окружность проходит через вершины \(A, B\) и \(C\) параллелограмма \(ABCD\), пересекает продолжение стороны \(AD\) за точку \(D\) в точке \(E\) и пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(K\).

а) Докажите, что \(BK=BE\).

б) Найдите отношение \(KE:AC\), если \(\angle BAD=30^{\circ}\).

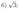
Окружность проходит через вершины \(A, B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(E\) и пересекает сторону \(CD\) в точках \(K\) и \(D\).

а) Докажите, что \(AE=AK\).

б) Найдите \(AD\), если \(CE=10, DK=9\) и \(\cos \angle BAD=0,2\).

Окружность проходит через вершины \(A, B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(E\) и пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(K\).

а) Докажите, что \(AE=AK\).

б) Найдите отношение \(KE:BD\), если \(\angle BAD=60^{\circ}\).

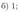
Окружность проходит через вершины \(A, B\) и \(D\) параллелограмма \(ABCD\), пересекает сторону \(BC\) в точках \(B\) и \(M\) и пересекает продолжение стороны \(CD\) за точку \(D\) в точке \(N\).

а) Докажите, что \(AM=AN\).

б) Найдите отношение \(CD:DN\), если \(AB:BC=1:2\), a \(\cos \angle BAD=\frac{2}{3}\).

Пятиугольник \(ABCDE\) вписан в окружность. Диагонали \(AD\) и \(BE\) пересекаются в точке \(M\). Известно, что \(BCDM\) — параллелограмм.

а) Докажите, что \(BC=DE\).

б) Найдите длину стороны \(AB\), если известно, что \(DE=4, AD=7, BE=8\) и \(AB>BC\).

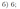
Периметр треугольника \(ABC\) равен 36. Точки \(E\) и \(F\) — середины сторон \(AB\) и \(BC\) соответственно. Отрезок \(EF\) касается окружности, вписанной в треугольник \(ABC\).

а) Докажите, что \(AC=9\).

б) Найдите площадь треугольника \(ABC\), если \(\angle ACB=90^{\circ}\).

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\).

б) Вычислите длину стороны \(BC\) и радиус данной окружности, если \(\angle A=30^{\circ}, B_1C_1=5\) и площадь треугольника \(AB_1C_1\) в пять раз меньше площади четырёхугольника \(BCB_1C_1\).

Диагонали равнобедренной трапеции \(ABCD\) с основаниями \(BC\) и \(AD\) перпендикулярны. Окружность с диаметром \(AD\) пересекает боковую сторону \(CD\) в точке \(M\), а окружность с диаметром \(CD\) пересекает основание \(AD\) в точке \(N\). Отрезки \(AM\) и \(CN\) пересекаются в точке \(P\).

а) Докажите, что в четырёхугольник \(ABCP\) можно вписать окружность.

б) Найдите радиус этой окружности, если \(BC=7, AD=23\).

Дана трапеция \(ABCD\) с основаниями \(AD\) и \(BC\). Диагональ \(BD\) разбивает её на два равнобедренных треугольника с основаниями \(AD\) и \(CD\).

а) Докажите, что луч \(AC\) — биссектриса угла \(BAD\).

б) Найдите \(CD\), если известны диагонали трапеции: \(AC=12\) и \(BD=6,5\).

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\).

б) Вычислите длину стороны \(BC\) и радиус данной окружности, если \(\angle A=45^{\circ}, B_1C_1=6\) и площадь треугольника \(AB_1C_1\) в восемь раз меньше площади четырёхугольника \(BCB_1C_1\).

Диагонали равнобедренной трапеции \(ABCD\) с основаниями \(BC\) и \(AD\) перпендикулярны. Окружность с диаметром \(AD\) пересекает боковую сторону \(CD\) в точке \(M\), а окружность с диаметром \(CD\) пересекает основание \(AD\) в точке \(N\). Отрезки \(AM\) и \(CN\) пересекаются в точке \(P\).

а) Докажите, что в четырёхугольник \(ABCP\) можно вписать окружность.

б) Найдите радиус этой окружности, если \(BC=7, AD=17\).

Точки \(P, Q, W\) делят стороны выпуклого четырёхугольника \(ABCD\) в отношении \(AP:PB=CQ:QB=CW:WD=3:4\), радиус окружности, описанной около треугольника \(PQW\), равен \(10, PQ=16, QW=12\), угол \(PWQ\) — острый.

а) Докажите, что треугольник \(PQW\) — прямоугольный.

б) Найдите площадь четырёхугольника \(ABCD\).

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.>

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\).

б) Вычислите длину стороны \(BC\) и радиус данной окружности, если \(\angle A=135^{\circ}, B_1C_1=10\) и площадь треугольника \(AB_1C_1\) в семь раз меньше площади четырёхугольника \(BCB_1C_1\).

Прямая, проходящая через середину \(M\) гипотенузы \(AB\) прямоугольного треугольника \(ABC\), перпендикулярна \(CM\) и пересекает катет \(AC\) в точке \(K\). При этом \(AK:KC=1:2\).

а) Докажите, что \(\angle BAC=30^{\circ}\).

б) Пусть прямые \(MK\) и \(BC\) пересекаются в точке \(P\), а прямые \(AP\) и \(BK\) — в точке \(Q\). Найдите \(KQ\), если \(BC=\sqrt{21}\).

Точки \(P, Q, W\) делят стороны выпуклого четырёхугольника \(ABCD\) в отношении \(AP:PB=CQ:QB=CW:WD=1:4\), радиус окружности, описанной около треугольника \(PQW\), равен \(10, PQ=16, QW=12\), угол \(PWQ\) — острый.

а) Докажите, что треугольник \(PQW\) — прямоугольный.

б) Найдите площадь четырёхугольника \(ABCD\).

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\).

б) Вычислите длину стороны \(B_1C_1\) и радиус данной окружности, если \(\angle A=150^{\circ}, BC=5\sqrt{5}\) и площадь треугольника \(AB_1C_1\) в четыре раза меньше площади четырёхугольника \(BCB_1C_1\).

Окружность проходит через вершины \(B\) и \(C\) треугольника \(ABC\) и пересекает \(AB\) и \(AC\) в точках \(C_1\) и \(B_1\) соответственно.

а) Докажите, что треугольник \(ABC\) подобен треугольнику \(AB_1C_1\).

б) Вычислите длину стороны \(B_1C_1\) и радиус данной окружности, если \(\angle A=120^{\circ}, BC=10\sqrt{7}\) и площадь треугольника \(AB_1C_1\) в три раза меньше площади четырёхугольника \(BCB_1C_1\).)

Прямая, проходящая через вершину \(B\) прямоугольника \(ABCD\) перпендикулярно диагонали \(AC\), пересекает сторону \(AD\) в точке \(M\), равноудалённой от вершин \(B\) и \(D\).

а) Докажите, что \(\angle ABM=\angle DBC=30^{\circ}\).

б) Найдите расстояние от центра прямоугольника до прямой \(CM\), если \(BC=9\).

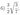
Дана трапеция \(ABCD\) с основаниями \(AD\) и \(BC\). Диагональ \(BD\) разбивает её на два равнобедренных треугольника с основаниями \(AD\) и \(CD\).

а) Докажите, что луч \(AC\) — биссектриса угла \(BAD\).

б) Найдите \(CD\), если известны диагонали трапеции: \(AC=15\) и \(BD=8,5\).

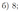
На сторонах \(AB, BC\) и \(AC\) треугольника \(ABC\) отмечены точки \(C_1, A_1\) и \(B_1\) соответственно, причём \(AC_1:C_1B=8:3\), \(BA_1:A_1C=1:2, AB_1:B_1C=1:3\). Отрезки \(BB_1\) и \(CC_1\) пересекаются в точке \(D\).

а) Докажите, что четырёхугольник \(ADA_1B_1\) — параллелограмм.

б) Найдите радиус окружности, описанной около треугольника \(ABC\), если отрезки \(AD\) и \(BC\) перпендикулярны, \(AC=16, BC=15\).

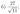
треугольнике \(ABC\) точки \(A_1, B_1\) и \(C_1\) — середины сторон \(BC, AC\) и \(AB\) соответственно, \(AH\) — высота, \(\angle BAC=60^{\circ}, \angle BCA=45^{\circ}\).

а) Докажите, что точки \(A_1, B_1, C_1\) и \(H\) лежат на одной окружности.

б) Найдите \(A_1H\), если \(BC=2\sqrt{3}\).

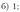
В трапеции \(ABCD\) основание \(AD\) в два раза больше основания \(BC\). Внутри трапеции взяли точку \(M\) так, что углы \(ABM\) и \(DCM\) прямые.

а) Докажите, что \(AM=DM\).

б) Найдите угол \(BAD\), если угол \(ADC\) равен \(70^{\circ}\), а расстояние от точки \(M\) до прямой \(AD\) равно стороне \(BC\).

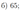
В треугольнике \(ABC\) угол \(A\) равен \(120^{\circ}\). Прямые, содержащие высоты \(BM\) и \(CN\) треугольника \(ABC\), пересекаются в точке \(H\). Точка \(O\) — центр окружности, описанной около треугольника \(ABC\).

а) Докажите, что \(AH=AO\).

б) Найдите площадь треугольника \(AHO\), если \(BC=\sqrt{15}, \angle ABC=45^{\circ}\).

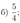
В равнобедренной трапеции \(ABCD\) основание \(AD\) в три раза больше основания \(BC\).

а) Докажите, что высота \(CH\) трапеции разбивает основание \(AD\) на отрезки, один из которых вдвое больше другого.

б) Найдите расстояние от вершины \(C\) до середины диагонали \(BD\), если \(AD=15\) и \(AC=2\sqrt{61}\).

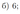
В трапеции \(ABCD\) угол \(BAD\) прямой. Окружность, построенная на большем основании \(AD\) как на диаметре, пересекает меньшее основание \(BC\) в точках \(C\) и \(M\).

а) Докажите, что \(\angle BAM=\angle CAD\).

б) Диагонали трапеции \(ABCD\) пересекаются в точке \(O\). Найдите площадь треугольника \(AOB\), если \(AB=\sqrt{10}\), а \(BC=2BM\).

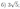
Высоты \(BB_1\) и \(CC_1\) остроугольного треугольника \(ABC\) пересекаются в точке \(H\).

а) Докажите, что \(\angle BB_1C_1=\angle BAH\).

б) Найдите расстояние от центра окружности, описанной около треугольника \(ABC\), до стороны \(BC\), если \(B_1C_1=18\) и \(\angle BAC=30^{\circ}\).

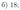
В треугольнике \(ABC\) точки \(A_1, B_1\) и \(C_1\) — середины сторон \(BC, AC\) и \(AB\) соответственно, \(AH\) — высота, \(\angle BAC=120^{\circ}, \angle BCA=45^{\circ}\).

а) Докажите, что точки \(A_1, B_1, C_1\) и \(H\) лежат на одной окружности.

б) Найдите \(A_1H\), если \(BC=6\sqrt{3}\).

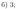
В прямоугольном треугольнике \(ABC\) точка \(M\) лежит на катете \(AC\), а точка \(N\) лежит на продолжении катета \(BC\) за точку \(C\), причём \(CM=BC\) и \(CN=AC\).

а) Отрезки \(CP\) и \(CQ\) — медианы треугольников \(ABC\) и \(NCM\) соответственно. Докажите, что прямые \(CP\) и \(CQ\) перпендикулярны.

б) Прямые \(MN\) и \(AB\) пересекаются в точке \(K\), а прямые \(BM\) и \(AN\) — в точке \(L\). Найдите \(KL\), если \(BC=1\), а \(AC=5\).

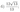
Пятиугольник \(ABCDE\) вписан в окружность. Известно, что \(AB=CD=3, BC=DE=4\).

а) Докажите, что \(AC=CE\).

б) Найдите длину диагонали \(BE\), если \(AD=6\).

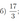
Сумма оснований трапеции равна 10, а её диагонали равны 6 и 8.

а) Докажите, что диагонали трапеции перпендикулярны.

б) Найдите высоту трапеции.

Две окружности касаются внутренним образом в точке \(C\). Вершины \(A\) и \(B\) равнобедренного прямоугольного треугольника \(ABC\) с прямым углом \(C\) лежат на меньшей и большей окружностях соответственно. Прямая \(AC\) вторично пересекает большую окружность в точке \(E\), а прямая \(BC\) вторично пересекает меньшую окружность в точке \(D\).

а) Докажите, что прямые \(AD\) и \(BE\) параллельны.

б) Найдите \(AC\), если радиусы окружностей равны 3 и 4.

В треугольнике \(ABC\) точки \(A_1, B_1\) и \(C_1\) — середины сторон \(BC, AC\) и \(AB\) соответственно, \(AH\) — высота, \(\angle BAC=30^{\circ}, \angle BCA=45^{\circ}\).

а) Докажите, что точки \(A_1, B_1, C_1\) и \(H\) лежат на одной окружности.

б) Найдите \(A_1H\), если \(BC=4\sqrt{3}\).

В треугольнике \(ABC\) точки \(A_1, B_1\) и \(C_1\) — середины сторон \(BC, AC\) и \(AB\) соответственно, \(AH\) — высота, \(\angle BAC=120^{\circ}, \angle BCA=15^{\circ}\).

а) Докажите, что точки \(A_1, B_1, C_1\) и \(H\) лежат на одной окружности.

б) Найдите \(A_1H\), если \(BC=4\sqrt{3}\).

Две окружности касаются внутренним образом в точке \(A\), причём меньшая проходит через центр большей. Хорда \(BC\) большей окружности касается меньшей в точке \(P\). Хорды \(AB\) и \(AC\) пересекают меньшую окружность в точках \(K\) и \(M\) соответственно.

а) Докажите, что прямые \(KM\) и \(BC\) параллельны.

б) Пусть \(L\) — точка пересечения отрезков \(KM\) и \(AP\). Найдите длину отрезка \(AL\), если радиус большей окружности равен 34, а \(BC=32\).

Две окружности разных радиусов касаются внешним образом в точке \(C\). Вершины \(A\) и \(B\) равнобедренного прямоугольного треугольника \(ABC\) с прямым углом \(C\) лежат на меньшей и большей окружностях соответственно. Прямая \(AC\) вторично пересекает большую окружность в точке \(E\), а прямая \(BC\) вторично пересекает меньшую окружность в точке \(D\).

а) Докажите, что прямые \(AD\) и \(BE\) параллельны.

б) Найдите \(BC\), если радиусы окружностей равны \(\sqrt{15}\) и 15.

Точка \(E\) — середина боковой стороны \(CD\) трапеции \(ABCD\). На стороне \(AB\) взяли точку \(K\) так, что прямые \(CK\) и \(AE\) параллельны. Отрезки \(CK\) и \(BE\) пересекаются в точке \(O\).

а) Докажите, что \(CO=KO\).

б) Найдите отношение оснований трапеции \(BC\) и \(AD\), если площадь треугольника \(BCK\) составляет \(\frac{9}{100}\) площади трапеции \(ABCD\).

В равнобедренной трапеции \(ABCD\) основание \(AD\) в два раза больше основания \(BC\).

а) Докажите, что высота \(CH\) трапеции разбивает основание \(AD\) на отрезки, один из которых втрое больше другого.

б) Пусть \(O\) — точка пересечения диагоналей трапеции \(ABCD\). Найдите расстояние от вершины \(C\) до середины отрезка \(OD\), если \(BC=16\) и \(AB=10\).

На сторонах \(AB, BC\) и \(AC\) треугольника \(ABC\) отмечены точки \(C_1, A_1\) и \(B_1\) соответственно, причём \(AC_1:C_1B=21:10\), \(BA_1:A_1C=2:3, AB_1:B_1C=2:5\). Отрезки \(BB_1\) и \(CC_1\) пересекаются в точке \(D\).

а) Докажите, что четырёхугольник \(ADA_1B_1\) — параллелограмм.

б) Найдите \(CD\), если отрезки \(AD\) и \(BC\) перпендикулярны, \(AC=63, BC=25\).

В треугольнике \(ABC\) угол \(A\) равен \(120^{\circ}\). Прямые, содержащие высоты \(BM\) и \(CN\) треугольника \(ABC\), пересекаются в точке \(H\). Точка \(O\) — центр окружности, описанной около треугольника \(ABC\).

а) Докажите, что \(AH=AO\).

б) Найдите площадь треугольника \(AHO\), если \(BC=3, \angle ABC=15^{\circ}\).

Окружность, вписанная в равнобедренную трапецию \(ABCD\), касается её боковой стороны \(CD\) в точке \(M\). Луч \(AM\) вторично пересекает окружность в точке \(N\), а прямую \(BC\) — в точке \(K\), причём \(AN=4, MN=12\).

а) Докажите, что \(\angle AMD=\angle MCK\).

б) Найдите основания трапеции.

Сумма оснований трапеции равна 13, а её диагонали равны 5 и 12.

а) Докажите, что диагонали трапеции перпендикулярны.

б) Найдите высоту трапеции.