Начать бесплатно

Меню

Подготовка к ЕГЭ

Бесплатные материалы

О нас

👋 Все программы

Успей присоединиться к Годовому курсу до старта

Лови выгоду!

от 5 499 руб.

математика

физика

информатика

русский язык

обществознание

Пиши «SCHOOL» и забронируй место. Экономия до 20 000 рублей

Места уходят каждый час!

Выбрать курс

Планиметрия

ЕГЭ 2019

Telegram основной

ВКонтакте

Telegram основной

Другие бесплатные материалы от Профиматики

Telegram для преподавателей

⬈

Наши соцсети:

Хочешь больше полезных материалов? Переходи по ссылкам

Задание 1

Katex Дана трапеция \(A B C D\) с основаниями \(B C\) и \(A D\). Точки \(M\) и \(N\) являются серединами сторон \(A B\) и \(C D\) соответственно. Окружность, проходящая через точки \(B\) и \(C\), пересекает отрезки \(B M\) и \(C N\) в точках \(P\) и \(Q\) (отличных от концов отрезков).
а) Докажите, что точки \(M, N, P\) и \(Q\) лежат на одной окружности.
б) Найдите \(Q N\), если отрезки \(D P\) и \(P C\) перпендикулярны, \(A B=21, B C=4, C D=\)\(=20, A D=17\).

Показать ответ и решение

Ответ:

Марафоны Профиматики

прокачай свои навыки решения сложных задач

Задание 2

Katex Дана трапеция \(A B C D\) с основаниями \(B C\) и \(A D\). Точки \(M\) и \(N\) являются серединами сторон \(A B\) и \(C D\) соответственно. Окружность, проходящая через точки \(B\) и \(C\), пересекает отрезки \(B M\) и \(C N\) в точках \(P\) и \(Q\) (отличных от концов отрезков).
а) Докажите, что точки \(M, N, P\) и \(Q\) лежат на одной окружности.
б) Найдите радиус окружности, описанной около треугольника \(M P Q\), если прямая \(D P\) перпендикулярна прямой \(P C, A B=25\), \(B C=3, C D=28, A D=20\).

Показать ответ и решение

Ответ:

Задание 3

Katex Дана трапеция \(A B C D\) с основаниями \(B C\) и \(A D\). Точки \(M\) и \(N\) являются серединами сторон \(A B\) и \(C D\) соответственно. Окружность, проходящая через точки \(B\) и \(C\), пересекает отрезки \(B M\) и \(C N\) в точках \(P\) и \(Q\) (отличных от концов отрезков).
а) Докажите, что точки \(M, N, P\) и \(Q\) лежат на одной окружности.
б) Найдите длину отрезка \(Q N\), если \(B C=4,5, A D=21,5, A B=26, C D=25\), а угол \(C P D\) -- прямой.

Показать ответ и решение

Ответ:

Задание 4

Katex Дана трапеция \(A B C D\) с основаниями \(A D\) и \(B C\). Точки \(M\) и \(N\) - середины сторон \(A B\) и \(C D\) соответственно. Окружность проходит через точки \(B\) и \(C\) и пересекает отрезки \(B M\) и \(C N\) в точках \(P\) и \(Q\), отличных от концов отрезка, соответственно.
а) Докажите, что точки \(M, N, P\) и \(Q\) лежат на одной окружности.
б) Найдите \(P M\), если отрезки \(A Q\) и \(B Q\) перпендикулярны, \(A B=15, B C=1, C D=\)\(=17, A D=9\).

Показать ответ и решение

Ответ:

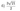
Задание 5

Katex Две окружности касаются внешним образом в точке \(K\). Прямая \(A B\) касается первой окружности в точке \(A\), а второй -- в точке \(B\). Прямая \(B K\) пересекает первую окружность в точке \(D\), прямая \(A K\) пересекает вторую окружность в точке \(C\).
а) Докажите, что прямые \(A D\) и \(B C\) параллельны.
б) Найдите радиус окружности, описанной около треугольника \(B C D\), если известно, что радиус первой окружности равен 4 , а радиус второй окружности равен 1.

Показать ответ и решение

Ответ:

Задание 6

Katex Точка \(O\) -- центр вписанной в треугольник \(A B C\) окружности. Прямая \(O B\) вторично пересекает описанную около этого треугольника окружность в точке \(P\).
а) Докажите, что \(O P=A P\).
б) Найдите расстояние от точки \(P\) до прямой \(A C\), если \(\angle A B C=120^{\circ}\), а радиус описанной окружности равен 18 .

Показать ответ и решение

Ответ:

Задание 7

Katex Около остроугольного треугольника \(A B C\) с различными сторонами описали окружность с диаметром \(B N\). Высота \(B H\) пересекает эту окружность в точке \(K\).
а) Докажите, что \(A N=C K\).
б) Найдите \(K N\), если \(\angle B A C=35^{\circ}, \angle A C B=65^{\circ}\), а радиус окружности равен 12 .

Показать ответ и решение

Ответ:

Задание 8

Katex Точка \(O\) -- центр вписанной в треугольник \(A B C\) окружности. Прямая \(O B\) вторично пересекает описанную около этого треугольника окружность в точке \(P\).
а) Докажите, что \(\angle P O C=\angle P C O\).
б) Найдите площадь треугольника \(A P C\), если радиус описанной около треугольника \(A B C\) окружности равен 4, а \(\angle A B C=120^{\circ}\).

Показать ответ и решение

Ответ:

Задание 9

Katex Точка \(O\) -- центр вписанной в треугольник \(A B C\) окружности. Прямая \(B O\) вторично пересекает описанную около этого треугольника окружность в точке \(P\).
а) Докажите, что \(\angle P O C=\angle P C O\).
б) Найдите площадь треугольника \(A P C\), если радиус описанной около треугольника \(A B C\) окружности равен 8, а \(\angle A B C=60^{\circ}\).

Показать ответ и решение

Ответ:

Задание 10

Katex В остроугольном треугольнике \(A B C, \angle A=60^{\circ}\). Высоты \(B N\) и \(C M\) треугольника \(A B C\) пересекаются в точке \(H\). Точка \(O\) центр окружности, описанной около \(\triangle A B C\).
а) Докажите, что \(A H=A O\).
б) Найдите площадь \(\triangle A H O\), если \(B C=6 \sqrt{3}, \angle A B C=45^{\circ}\).

Показать ответ и решение

Ответ:

Задание 11

Katex В прямоугольном треугольнике \(A B C\) точка \(M\) лежит на катете \(A C\), а точка \(N\) лежит на продолжении катета \(B C\) за точку \(C\), причём \(C M=B C\) и \(C N=A C\). Отрезки \(C P\) и \(C Q\) - биссектрисы треугольников \(A C B\) и \(N C M\) соответственно.
а) Докажите, что \(C P\) и \(C Q\) перпендикулярны.
б) Найдите \(P Q\), если \(B C=3\), а \(A C=5\).

Показать ответ и решение

Ответ:

Задание 12

Katex Окружность касается стороны \(A C\) остроугольного треугольника \(A B C\) и делит каждую из сторон \(A B\) и \(B C\) на три равные части.
а) Докажите, что треугольник \(A B C\) равнобедренный.
б) Найдите, в каком отношении высота этого треугольника делит сторону \(B C\).

Показать ответ и решение

Ответ:

Задание 13

Katex Из вершины \(C\) прямого угла прямоугольного треугольника \(A B C\) проведена высота \(C H\).
а) Докажите, что отношение площадей кругов, построенных на отрезках \(A H\) и \(B H\) соответственно как на диаметрах равно \(\operatorname{tg}^4 \angle A B C\).
б) Пусть точка \(O_1\) -- центр окружности диаметра \(A H\), вторично пересекающей отрезок \(A C\) в точке \(P\), а точка \(O_2\) -- центр окружности с диаметром \(B H\), вторично пересекающей отрезок \(B C\) в точке \(Q\). Найдите площадь четырёхугольника \(O_1 P Q O_2\), если \(A C=22, B C=18\).

Показать ответ и решение

Ответ:

Задание 14

Katex Две окружности разных радиусов касаются внешним образом в точке \(K\). Прямая касается первой окружности в точке \(A\), а второй окружности в точке \(B\). Луч \(B K\) пересекает первую окружность в точке \(D\), луч \(A K\) пересекает вторую окружность в точке \(C\).
а) Докажите, что четырёхугольник \(A B C D\) -- трапеция.
б) Найдите радиус окружности, описанной около треугольника \(B C D\), если радиус первой окружности равен 1, а радиус второй окружности равен 4.

Показать ответ и решение

Ответ:

⚡️ протестируй свой уровень
⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ

Бесплатный пробный урок любого курса