В треугольнике \(ABC\) угол \(C\) равен \(90{}^\circ\), \(AC=25\), \(\sin A=\dfrac{12}{13}\). Найдите \(BC\).

В четырёхугольник \(ABCD\) вписана окружность, \(AB=7\), \(CD=13\). Найдите периметр четырёхугольника \(ABCD\).

Наблюдатель находится на высоте \(h\), выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле \(l = \sqrt {\frac{Rh}{500}}\), где \(R = 6400\) км - радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии \(172\) километров? Ответ дайте в метрах.

Зависимость объёма спроса \(q\) (единиц в месяц) на продукцию предприятия-монополиста от цены \(p\) (тыс.~руб. за ед.) задаётся формулой \(q=75-5p\). Выручка предприятия \(r\) (в тыс. руб. за месяц) вычисляется по формуле \(r(p)=q\cdot p\). Определите наибольшую цену \(p\), при которой месячная выручка \(r(p)\) составит не менее \(180\) тыс. руб. Ответ дайте в тыс. руб. за ед.

При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями \(u\) и \(v\) (в м/с) соответственно, частота звукового сигнала \(f\) (в Гц), регистрируемого приёмником, вычисляется по формуле \(f=f_0\cdot \frac{c+u}{c-v}\), где \(f_0=150\) Гц — частота исходного сигнала, \(c\) — скорость распространения сигнала в среде (в м/с), а \(u = 13\) м/с и \(v = 6\) м/с — скорости источника и приёмника относительно среды. При какой скорости распространения сигнала в среде частота сигнала в приёмнике будет равна \(155\) Гц? Ответ дайте в м/с.

Первый час автомобиль ехал со скоростью \(120\) км/ч, следующие три часа - со скоростью \(105\) км/ч, а затем три часа - со скоростью \(65\) км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

На рисунке изображён график функции вида \(f(x)=\log_ax\). Найдите значение \(f(25)\).

Найдите точку максимума функции \(y=-\dfrac{x^2 +400}{x}\).

Найдите точку минимума функции \(y=\left(6-4x\right)\cos x +4\sin x+9\) принадлежащую промежутку \(\left(0;\dfrac{\pi}{2}\right)\).

а) Решите уравнение

а) Решите уравнение

Прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\), два сечения \(AOB\) и \(BOC\) - являются прямоугольниками. Точка \(O\) центр грани \(A_1B_1C_1D_1\). Известно, что каждая из плоскостей является прямоугольником, у которых стороны \(AB\) и \(BC\) - это меньшие стороны и они в \(2\) раза меньше двух других сторон.

a) Доказать, что \(ABCD\) - квадрат.

б) Найти угол между плоскостью \(BOC\) и \(CA_1\).

Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\). Через прямую \(BD_1\) параллельно прямой \(AC\) проведена плоскость \(\pi\), причём сечение параллелепипеда плоскостью \(\pi\) представляет собой ромб.

a) Докажите, что \(ABCD\) - квадрат.

б) Найти угол между плоскостью \(\pi\) и плоскостью \((BCC_1)\), если \(AD=4\) и \(AA_1=6\).

Решите неравенство

Решите неравенство

Зависимость объёма \(Q\) (в шт.) купленного у фирмы товара от цены \(Р\) (в руб. за шт.) выражается формулой \(Q=15000-P\), \(1000\leq P\leq 15000\). Доход от продажи товара составляет \(РQ\) рублей. Затраты на производство \(Q\) единиц товара составляют \(3000Q+5000000\) рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену товара на \(20\%\), однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?

Зависимость количества \(Q\) (в шт., \(0\leq Q \leq 15000\)) купленного у фирмы товара от цены \(P\) (в руб. за шт.) выражается формулой \(Q=15000-P\). Затраты на производство \(Q\) единиц товара составляют \(3000Q+1000000\) рублей. Кроме затрат на производство, фирма должна платить налог \(t\) рублей \((0< t < 10000)\) с каждой произведённой единицы товара. Таким образом, прибыль фирмы составляет \(PQ-3000Q-1000000-tQ\) рублей, а общая сумма налогов, собранных государством, равна \(t Q\) рублей.

Фирма производит такое количество товара, при котором её прибыль максимальна. При каком значении \(t\) общая сумма налогов, собранных государством, будет максимальной?

Дан ромб \(ABCD\). На диагонали \(AC\) отмечены точки \(M\) и \(N\) так, что \(AM = MN = NC\). Прямая \(BM\) пересекает сторону \(AD\) в точке \(P\), а прямая \(BN\) пересекает сторону \(CD\) в точке \(Q\).

a) Докажите, что площадь четырехугольника \(BPDQ\) равна площади треугольника \(ADC\).

б) Найдите \(BD\), если известно, что \(AC = 2\sqrt{3}\) и около пятиугольника \(MNQDP\) можно описать окружность.

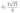
Дан ромб \(ABCD\). Точки \(P\) и \(Q\) - середины сторон \(BC\) и \(CD\) соответственно. Проведены \(AP\) и \(AQ\) таким образом, что они пересекают диагональ \(BD\) в точках \(M\) и \(N\) соответственно.

a) Докажите, что сумма площадей треугольников \(BMP\) и \(DNQ\) равна площади треугольника \(AMN\).

б) Известно, что в \(CPMNQ\) можно вписать окружность. Найдите радиус этой окружности, если сторона ромба равна \(12\sqrt{5}\).

Найдите все значения параметра \(a\), при каждом из которых система уравнений

На доске написано \(24\) числа: восемь «\(5\)», восемь «\(4\)» и восемь «\(3\)». Эти числа разбивают на две группы, в каждой из которых есть хотя бы одно число. Среднее арифметическое чисел в первой группе равно \(A\), среднее арифметическое чисел во второй группе равно \(B\). При этом для группы из единственного числа среднее арифметическое равно этому числу.

a) Приведите пример разбиения исходных чисел на две группы, при котором среднее арифметическое всех чисел меньше \(\dfrac{A+B}{2}\).

б) Докажите, что если разбить исходные числа на две группы по \(12\) чисел, то среднее арифметическое всех чисел будет равно \(\dfrac{A+B}{2}\).

в) Найдите наибольшее возможное значение выражения \(\dfrac{A+B}{2}\).