Стереометрия

ЕГЭ 2017

Telegram основной

ВКонтакте

Telegram основной

Другие бесплатные материалы от Профиматики

Telegram для преподавателей

⬈

Наши соцсети:

Хочешь больше полезных материалов? Переходи по ссылкам

Задание 1

Katex Основанием прямой треугольной призмы \(A B C A_1 B_1 C_1\) является прямоугольный треугольник \(A B C\) с прямым углом \(C\). Грань \(A C C_1 A_1\) является квадратом.
a) Докажите, что прямые \(C A_1\) и \(A B_1\) перпендикулярны.
б) Найдите расстояние между прямыми \(C A_1\) и \(A B_1\), если \(A C=4, B C=7\).

Показать ответ и решение

+

Ответ:

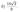
Задание 2

Katex Дана четырёхугольная пирамида \(S A B C D\) с прямоугольником \(A B C D\) в основании. Сторона \(A B\) равна \(3 \sqrt{2}\), а \(B C\) равна 6 . Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин \(A\) и \(C\) на ребро \(S B\) опущены перпендикуляры \(A P\) и \(C Q\).
a) Докажите, что точка \(P\) является серединой отрезка \(B Q\).
б) Найдите угол между плоскостями \(S B A\) и \(S B C\), если ребро \(S D\) равно 9.

Показать ответ и решение

+

Ответ:

Задание 3

Katex Дана четырёхугольная пирамида \(S A B C D\) с прямоугольником \(A B C D\) в основании. Сторона \(A B\) равна 4 , а \(B C\) равна \(4 \sqrt{2}\). Вершина пирамиды \(S\) проецируется в точку пересечения диагоналей прямоугольника. Из вершины \(A\) и \(C\) на ребро \(S B\) опущены перпендикуляры \(A P\) и \(C Q\).
a) Докажите, что точка \(P\) является серединой отрезка \(B Q\).
б) Найдите угол между плоскостями \(S B A\) и \(S B C\), если ребро \(S D\) равно 8.

Показать ответ и решение

+

Ответ:

Задание 4

Katex Основанием прямой треугольной призмы \(A B C A_1 B_1 C_1\) является прямоугольный треугольник \(A B C\) с прямым углом \(C\). Диагонали боковых граней \(A A_1 B_1 B\) и \(B B_1 C_1 C\) равны 15 и 9 соответственно, \(A B=13\).
a) Докажите, что треугольник \(B A_1 C_1\) прямоугольный.
б) Найдите объём пирамиды \(A A_1 C_1 B\).

Показать ответ и решение

+

Ответ:

Марафоны Профиматики

прокачай свои навыки решения сложных задач

Задание 5

Katex Дана пирамида \(P A B C D\), в основании -- трапеция \(A B C D\) с большим основанием \(A D\). Известно, что сумма углов \(B A D\) и \(A D C\) равна \(90^{\circ}\), а плоскости \(P A B\) и \(P C D\) перпендикулярны основанию, прямые \(A B\) и \(C D\) пересекаются в точке \(K\).
a) Доказать, что плоскость \(P A B\) перпендикулярна плоскости \(P C D\).
б) Найдите объём \(P K B C\), если \(A B=B C=C D=2\), а \(P K=12\).

Показать ответ и решение

+

Ответ:

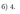
Задание 6

Katex Дана пирамида \(P A B C D\), в основании - трапеция \(A B C D\) с большим основанием \(A D\). Известно, что сумма углов \(B A D\) и \(A D C\) равна 90 градусов, а плоскости \(P A B\) и \(P C D\) перпендикулярны основанию, прямые \(A B\) и \(C D\) пересекаются в точке \(K\).
a) Доказать, что плоскость \(P A B\) перпендикулярна плоскости \(P C D\).
б) Найдите объём \(P K B C\), если \(A B=B C=C D=3\), а \(P K=8\).

Показать ответ и решение

+

Ответ:

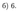
Задание 7

Katex Дана правильная четырёхугольная пирамида \(S A B C D\) с вершиной \(S\). Точка \(M\) расположена на \(S D\) так, что \(S M: S D=2: 3 . P-\) середина ребра \(A D\), а \(Q\) середина ребра \(B C\).
a) Докажите, что сечение пирамиды плоскостью \(M Q P\) - равнобедренная трапеция.
б) Найдите отношение объёмов многогранников, на которые плоскость \(M Q P\) разбивает пирамиду.

Показать ответ и решение

+

Ответ:

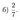
Задание 8

Katex Основанием прямой треугольной призмы \(A B C A_1 B_1 C_1\) является прямоугольный треугольник \(A B C\) с прямым углом \(C\). Прямые \(C A_1\) и \(A B_1\) перпендикулярны.
a) Докажите, что \(A A_1=A C\).
б) Найдите расстояние между прямыми \(C A_1\) и \(A B_1\), если \(A C=6, B C=3\).

Показать ответ и решение

+

Ответ:

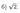
Задание 9

Katex На рёбрах \(A B\) и \(B C\) треугольной пирамиды \(A B C D\) отмечены точки \(M\) и \(N\) соответственно, причём \(A M: B M=C N: N B=1: 2\). Точки \(P\) и \(Q\) - середины ребер \(D A\) и \(D C\) соответственно.
a) Докажите, что \(P, Q, M\) и \(N\) лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость \(P Q M\) разбивает пирамиду.

Показать ответ и решение

+

Ответ:

Задание 10

Katex В треугольной пирамиде \(S A B C\) известны боковые рёбра: \(S A=S B=13, S C=3 \sqrt{17}\). Основанием высоты этой пирамиды является середина медианы \(C M\) треугольника \(A B C\). Эта высота равна 12 .
a) Докажите, что треугольник \(A B C\) равнобедренный.
б) Найдите объём пирамиды \(S A B C\).

Показать ответ и решение

+

Ответ:

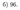
Задание 11

Katex В треугольной пирамиде \(S A B C\) известны боковые рёбра: \(S A=S B=7, S C=5\). Основанием высоты этой пирамиды является середина медианы \(C M\) треугольника \(A B C\). Эта высота равна 4.
a) Докажите, что треугольник \(A B C\) равнобедренный.
б) Найдите объём пирамиды \(S A B C\).

Показать ответ и решение

+

Ответ:

Задание 12

Katex Ребро куба \(A B C D A_1 B_1 C_1 D_1\) равно 6 . Точки \(K, L\) и \(M\) - центры граней \(A B C D, A A_1 D_1 D\) и \(C C_1 D_1 D\) соответственно.
a) Докажите, что \(B_1 K L M\) - правильная пирамида.
б) Найдите объём \(B_1 K L M\).

\newpage

Показать ответ и решение

+

Ответ:

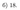
Задание 13

Katex На рёбрах \(A B\) и \(B C\) треугольной пирамиды \(A B C D\) отмечены точки \(M\) и \(N\) соответственно, причём \(A M: B M=C N: N B=1: 2\). Точки \(P\) и \(Q\) - середины ребер \(D A\) и \(D C\) соответственно.
a) Докажите, что \(P, Q, M\) и \(N\) лежат в одной плоскости.
б) Найти отношение объёмов многогранников, на которые плоскость \(P Q M\) разбивает пирамиду.

Показать ответ и решение

+

Ответ:

Задание 14

Katex Основанием прямой треугольной призмы \(A B C A_1 B_1 C_1\) является прямоугольный треугольник \(A B C\) с прямым углом \(C\). Диагонали боковых граней \(A A_1 B_1 B\) и \(B B_1 C_1 C\) равны 15 и 9 соответственно, \(A B=13\).
a) Докажите, что треугольник \(B A_1 C_1\) прямоугольный.
б) Найдите объём пирамиды \(A A_1 C_1 B\).

Показать ответ и решение

+

Ответ:

Задание 15

Katex В треугольной пирамиде \(P A B C\) с основанием \(A B C\) известно, что \(A B=13, P B=15, \cos \angle P B A=\frac{48}{65}\). Основанием высоты этой пирамиды является точка \(C\). Прямые \(P A\) и \(B C\) перпендикулярны.
a) Докажите, что треугольник \(A B C\) прямоугольный.
б) Найдите объем пирамиды \(P A B C\).

Показать ответ и решение

+

Ответ:

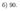
Задание 16

Katex В треугольной пирамиде \(P A B C\) с основанием \(A B C\) известно, что \(A B=17, P B=10, \cos \angle P B A=\frac{32}{85}\). Основанием высоты этой пирамиды является точка \(C\). Прямые \(P A\) и \(B C\) перпендикулярны.
a) Докажите, что треугольник \(A B C\) прямоугольный.
б) Найдите объем пирамиды \(P A B C\).

Показать ответ и решение

+

Ответ:

⚡️ протестируй свой уровень
⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ

Бесплатный пробный урок любого курса