Стереометрия

На ребре \(AA_1\) прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\) взята точка \(E\) так, что \(A_1E : EA = 1 : 2\), на ребре \(BB_1\) — точка \(F\) так, что \(B_1F : FB = 1 : 5\), а точка \(T\) — середина ребра \(B_1C_1\). Известно, что \(AB = 2\), \(AD = 6\), \(AA_1 = 6\).

а) Докажите, что плоскость \(EFT\) проходит через вершину \(D_1\)

б) Найдите угол между плоскостью \(E F T\) и плоскостью \(A A_1 B_1\).

Сечением прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\) плоскостью \(\alpha\), содержащей прямую \(BD_1\) и параллельной прямой \(AC\), является ромб.

а) Докажите, что грань \(ABCD\) — квадрат.

б) Найдите угол между плоскостями \(\alpha\) и \(BCC_1\), если \(AA_1=10, AB=12\).

B прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) известны длины рёбер: \(AB=6\sqrt{2}\), \(AD=10\), \(AA_1=16\). На рёбрах \(AA_1\) и \(BB_1\) отмечены точки \(E\) и \(F\) соответственно, причём \(A_1E:EA=5:3\) и \(B_1F:FB=5:11\). Точка \(T\) — середина ребра \(B_1C_1\).

а) Докажите, что плоскость \(EFT\) проходит через точку \(D_1\).

б) Найдите площадь сечения параллелепипеда плоскостью \(EFT\).

В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) через середину \(M\) диагонали \(AC_1\) проведена плоскость \(\alpha\) перпендикулярно этой диагонали, \(AB=5, BC=3, AA_1=4\).

а) Докажите, что плоскость \(\alpha\) содержит точку \(D_1\).

б) Найдите отношение, в котором плоскость \(\alpha\) делит ребро \(A_1B_1\).

В прямоугольном параллелепипеде \(ABCDA_1B_1C_1D_1\) известны длины рёбер: \(AB=2\sqrt{2}, AD=6\), \(AA_1=10\). На рёбрах \(AA_1\) и \(BB_1\) отмечены точки \(E\) и \(F\) соответственно, причём \(A_1E:EA=3:2\) и \(B_1F:FB=3:7\). Точка \(T\) — середина ребра \(B_1C_1\).

а) Докажите, что плоскость \(EFT\) проходит через точку \(D_1\).

б) Найдите площадь сечения параллелепипеда плоскостью \(EFT\).

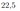
Сечением прямоугольного параллелепипеда \(ABCDA_1B_1C_1D_1\) плоскостью \(\alpha\), содержащей прямую \(BD_1\) и параллельной прямой \(AC\), является ромб.

а) Докажите, что грань \(ABCD\) — квадрат.

б) Найдите угол между плоскостями \(\alpha\) и \(BCC_1\), если \(AA_1=6, AB=4\).

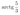
В кубе \(ABCDA_1B_1C_1D_1\) точки \(M\) и \(N\) — середины рёбер \(AB\) и \(AD\) соответственно.

а) Докажите, что прямые \(B_1N\) и \(CM\) перпендикулярны.

б) Плоскость \(\alpha\) проходит через точки \(N\) и \(B_1\) параллельно прямой \(CM\). Найдите расстояние от точки \(C\) до плоскости \(\alpha\), если \(B_1N=6\).

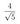
В основании правильной треугольной пирамиды \(ABCD\) лежит треугольник \(ABC\) со стороной, равной 6. Боковое ребро пирамиды равно 5. На ребре \(AD\) отмечена точка \(T\) так, что \(AT:TD=2:1\). Через точку \(T\) параллельно прямым \(AC\) и \(BD\) проведена плоскость.

а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.

б) Найдите площадь сечения.

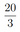
В основании правильной треугольной пирамиды \(ABCD\) лежит треугольник \(ABC\) со стороной, равной 5. Боковое ребро пирамиды равно 9. На ребре \(AD\) отмечена точка \(T\) так, что \(AT:TD=1:2\). Через точку \(T\) параллельно прямым \(AC\) и \(BD\) проведена плоскость.

а) Докажите, что сечение пирамиды указанной плоскостью является прямоугольником.

б) Найдите площадь сечения.

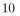
В основании пирамиды \(SABCD\) лежит прямоугольник \(ABCD\) со стороной \(AB=5\) и диагональю \(BD=9\). Все боковые рёбра пирамиды равны 5. На диагонали \(BD\) основания \(ABCD\) отмечена точка \(E\), а на ребре \(AS\) — точка \(F\) так, что \(SF=BE=4\).

а) Докажите, что плоскость \(CEF\) параллельна ребру \(SB\).

б) Плоскость \(CEF\) пересекает ребро \(SD\) в точке \(Q\). Найдите расстояние от точки \(Q\) до плоскости \(ABC\).

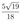
В основании пирамиды \(SABCD\) лежит трапеция \(ABCD\) с большим основанием \(AD\). Диагонали трапеции пересекаются в точке \(O\). Точки \(M\) и \(N\) — середины боковых сторон \(AB\) и \(CD\) соответственно. Плоскость \(\alpha\) проходит через точки \(M\) и \(N\) параллельно прямой \(SO\).

а) Докажите, что сечение пирамиды \(SABCD\) плоскостью \(\alpha\) является трапецией.

б) Найдите площадь сечения пирамиды \(SABCD\) плоскостью \(\alpha\), если \(AD=10, BC=8\), \(SO=8\), а прямая \(SO\) перпендикулярна прямой \(AD\).

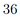
В правильной шестиугольной пирамиде \(SABCDEF\) сторона основания \(AB\) равна \(2\), а боковое ребро \(SA\) равно \(8\). Точка \(M\) — середина ребра \(АВ\). Плоскость \(\alpha\) перпендикулярна плоскости \(ABC\) и содержит точки \(M\) и \(D\). Прямая \(SC\) пересекает плоскость \(\alpha\) в точке \(K\).

а) Докажите, что \(KM = KD\).

б) Найдите объём пирамиды \(CDKM\).

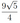
Основанием четырёхугольной пирамиды \(SABCD\) является прямоугольник \(ABCD\), причём \(AB=2\sqrt{2}, BC=4\). Основанием высоты пирамиды является центр прямоугольника. Из вершин \(A\) и \(C\) опущены перпендикуляры \(AP\) и \(CQ\) на ребро \(SB\).

а) Докажите, что \(P\) — середина отрезка \(BQ\).

б) Найдите угол между гранями \(SBA\) и \(SBC\), если \(SD=4\).

В правильной четырёхугольной пирамиде \(SABCD\) сторона основания \(AB\) равна 8, а боковое ребро \(SA\) равно 7. На рёбрах \(AB\) и \(SB\) отмечены точки \(M\) и \(K\) соответственно, причём \(AM=2\), \(SK=1\).

а) Докажите, что плоскость \(CKM\) перпендикулярна плоскости \(ABC\).

б) Найдите объём пирамиды \(BCKM\).

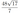
В правильной четырехугольной пирамиде \(SABCD\) сторона основания \(AB\) равна 8, а боковое ребро \(SA\) равно \(7\). На ребрах \(AB\) и \(SB\) отмечены точки \(M\) и \(K\) соответственно, причем \(AM=2\), \(SK=1\). Плоскость \(\alpha\) перпендикулярна плоскости \(ABC\) и содержит точки \(M\) и \(K\).

а) Докажите, что плоскость \(\alpha\) содержит точку \(C\).

б) Найдите площадь сечения пирамиды \(SABCD\) плоскостью \(\alpha\).

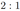
В правильной четырёхугольной пирамиде \(SABCD\) сторона основания \(AB\) равна 6, а боковое ребро \(SA\) равно 7. На рёбрах \(CD\) и \(SC\) отмечены точки \(N\) и \(K\) соответственно, причём \(DN:NC=SK:KC=1:2\). Плоскость \(\alpha\) содержит прямую \(KN\) и параллельна прямой \(BC\).

а) Докажите, что плоскость \(\alpha\) параллельна прямой \(SA\).

б) Найдите угол между плоскостями \(\alpha\) и \(SBC\).

В правильной треугольной пирамиде \(SABC\) сторона основания \(AB\) равна 6, а боковое ребро \(SA\) равно \(\sqrt{21}\). На рёбрах \(AB\) и \(SB\) отмечены точки \(M\) и \(K\) соответственно, причём \(AM=4\), \(SK:KB=1:3\).

а) Докажите, что плоскость \(CKM\) перпендикулярна плоскости \(ABC\).

б) Найдите объём пирамиды \(BCKM\).

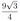
В правильной шестиугольной пирамиде \(S A B C D E F\) сторона основания \(A B\) равна 5, а боковое ребро \(S A\) равно 9. Точка \(M\) лежит на ребре \(A B, A M=1\), а точка \(K\) лежит на ребре \(S C\). Известно, что \(M K=K D\).

а) Докажите, что плоскость \(D K M\) перпендикулярна плоскости \(A B C\).

б) Найдите площадь треугольника \(D K M\).

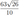
В основании пирамиды \(S A B C D\) лежит трапеция \(A B C D\) с основаниями \(A D\) и \(B C\), равными 8 и 3 соответственно. Точки \(M\) и \(N\) лежат на рёбрах \(S D\) и \(B C\) соответственно, причём \(S M: M D=3: 2, B N: N C=1: 2\). Плоскость \(A M N\) пересекает ребро \(S C\) в точке \(K\).

а) Докажите, что \(S K: K C=6: 1\).

б) Плоскость \(A M N\) делит пирамиду \(S A B C D\) на два многогранника. Найдите отношение их объёмов.

На ребре \(S D\) правильной четырёхугольной пирамиды \(S A B C D\) с основанием \(A B C D\) отмечена точка \(M\), причём \(S M: M D=2: 1\). Точки \(P\) и \(Q\) -- середины рёбер \(B C\) и \(A D\) соответственно.

a) Докажите, что сечение пирамиды плоскостью \(M P Q\) является равнобедренной трапецией.

б) Найдите отношение объёмов многогранников, на которые плоскость \(M P Q\) разбивает пирамиду.

На рёбрах \(A C, A D, B D\) и \(B C\) тетраэдра \(A B C D\) отмечены точки \(K, L, M\) и \(N\) соответственно, причём \(A K: K C=2: 3\). Четырёхугольник \(K L M N\) — квадрат со стороной 2.

а) Докажите, что прямые \(A B\) и \(C D\) перпендикулярны.

б) Найдите расстояние от вершины \(B\) до плоскости \(K L M\), если объём тетраэдра \(A B C D\) равен 25.

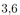
На рёбрах \(A B\) и \(B C\) треугольной пирамиды \(A B C D\) отмечены точки \(M\) и \(N\) соответственно, причём \(A M: M B=C N: N B=1: 2\). Точки \(P\) и \(Q\) — середины рёбер \(D A\) и \(D C\) соответственно.

а) Докажите, что точки \(P, Q, M\) и \(N\) лежат в одной плоскости.

б) Найдите отношение объёмов многогранников, на которые плоскость \(P Q M\) разбивает пирамиду.

В правильной четырёхугольной пирамиде \(S A B C D\) сторона основания \(A B\) равна 4, а боковое ребро \(S A\) равно 7. На рёбрах \(C D\) и \(S C\) отмечены точки \(N\) и \(K\) соответственно, причём \(D N: N C=S K: K C=1: 3\). Плоскость \(\alpha\) содержит прямую \(K N\) и параллельна прямой \(B C\).

а) Докажите, что плоскость \(\alpha\) параллельна прямой \(S A\).

б) Найдите угол между плоскостями \(\alpha\) и \(S B C\).

В пирамиде \(A B C D\) рёбра \(D A, D B\) и \(D C\) попарно перпендикулярны, a \(A B=B C=A C=5 \sqrt{2}\).

а) Докажите, что эта пирамида правильная.

б) На рёбрах \(D A\) и \(D C\) отмечены точки \(M\) и \(N\) соответственно, причем \(D M: M A=D N: N C=2: 3\). Найдите площадь сечения \(M N B\)

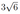
В пирамиде \(A B C D\) рёбра \(D A, D B\) и \(D C\) попарно перпендикулярны, а \(A B=B C=A C=6 \sqrt{2}\).

а) Докажите, что эта пирамида правильная.

б) На рёбрах \(D A\) и \(D C\) отмечены точки \(M\) и \(N\) соответственно, причём \(D M: M A=D N: N C=1: 2\). Найдите расстояние от точки \(D\) до плоскости \(M N B\).

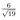
Основанием четырёхугольной пирамиды \(P A B C D\) является трапеция \(A B C D\), причём \(\angle B A D+\angle A D C=90^{\circ}\). Плоскости \(P A B\) и \(P C D\) перпендикулярны плоскости основания, \(K\) — точка пересечения прямых \(A B\) и \(C D\).

а) Докажите, что плоскости \(P A B\) и \(P C D\) перпендикулярны.

б) Найдите объём пирамиды \(K B C P\), если \(A B=B C=C D=4\), а высота пирамиды \(P A B C D\) равна 9.

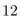
Точка \(M\) — середина ребра \(S A\) правильной четырёхугольной пирамиды \(S A B C D\) с основанием \(A B C D\). Точка \(N\) лежит на ребре \(S B, S N: N B=1: 2\).

а) Докажите, что плоскость \(C M N\) параллельна прямой \(S D\).

б) Найдите площадь сечения пирамиды \(S A B C D\) плоскостью \(C M N\), если все рёбра пирамиды равны 6.

Точка \(M\) — середина бокового ребра \(S C\) правильной четырёхугольной пирамиды \(S A B C D\). Точка \(N\) лежит на стороне основания \(B C\). Плоскость \(\alpha\) проходит через точки \(M\) и \(N\) параллельно боковому ребру \(S A\).

а) Плоскость \(\alpha\) пересекает боковое ребро \(S D\) в точке \(L\). Докажите, что \(B N: N C=D L: L S\).

б) Плоскость \(\alpha\) делит пирамиду \(S A B C D\) на два многогранника. Найдите отношение их объёмов, если \(B N: N C=1: 3\).

В правильной четырёхугольной пирамиде \(S A B C D\) с основанием \(A B C D\) точка \(O\) — центр основания пирамиды, точка \(M\) — середина ребра \(S C\), точка \(K\) делит ребро \(B C\) в отношении \(B K: K C=3: 1\), а \(A B=2\) и \(S O=\sqrt{14}\).

а) Докажите, что плоскость \(O M K\) параллельна прямой \(S A\).

б) Найдите длину отрезка, по которому плоскость \(O M K\) пересекает грань \(S A D\).

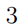
Все рёбра правильной четырёхугольной пирамиды \(S A B C D\) с основанием \(A B C D\) равны 4. Точка \(O\) — центр основания пирамиды. Плоскость, параллельная прямой \(S A\) и проходящая через точку \(O\), пересекает рёбра \(S C\) и \(S D\) в точках \(M\) и \(N\) соответственно. Точка \(N\) делит ребро \(S D\) в отношении \(S N: N D=1: 3\).

а) Докажите, что точка \(M\) — середина ребра \(S C\).

б) Найдите длину отрезка, по которому плоскость \(O M N\) пересекает грань \(S B C\).

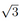
В правильной треугольной пирамиде \(S A B C\) с основанием \(A B C\) точки \(M\) и \(K\) — середины рёбер \(A B\) и \(S C\) соответственно, а точки \(N\) и \(L\) отмечены на рёбрах \(S A\) и \(B C\) соответственно так, что отрезки \(M K\) и \(N L\) пересекаются, а \(2A N=3 N S\).

а) Докажите, что прямые \(M N, K L\) и \(S B\) пересекаются в одной точке.

б) Найдите отношение \(B L: L C\).

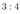
В правильной треугольной пирамиде \(S A B C\) с основанием \(A B C\) точки \(M\) и \(K\) — середины рёбра \(A B\) и \(S C\) соответственно. На продолжении ребра \(S B\) за точку \(S\) отмечена точка \(R\). Прямые \(R M\) и \(R K\) пересекают рёбра \(A S\) и \(B C\) в точках \(N\) и \(L\) соответственно, причём \(2B L=3 L C\).

а) Докажите, что отрезки \(M K\) и \(N L\) пересекаются.

б) Найдите отношение \(A N: N S\).

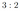
В правильном тетраэдре \(A B C D\) точки \(M\) и \(N\) — середины рёбер \(A B\) и \(C D\) соответственно. Плоскость \(\alpha\) перпендикулярна прямой \(M N\) и пересекает ребро \(B C\) в точке \(K\).

а) Докажите, что прямая \(M N\) перпендикулярна рёбрам \(A B\) и \(C D\).

б) Найдите площадь сечения тетраэдра \(A B C D\) плоскостью \(\alpha\), если известно, что \(B K=1, K C=3\).

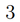
B правильной треугольной призме \(A B C A_1 B_1 C_1\) известно, что \(A B=2\). Плоскость \(\alpha\) проходит через вершины \(A_1\) и \(B\) и середину \(M\) ребра \(C C_1\).

а) Докажите, что сечение призмы \(A B C A_1 B_1 C_1\) плоскостью \(\alpha\) является равнобедренным треугольником.

б) Найдите высоту призмы, если площадь сечения плоскостью \(\alpha\) равна 6.

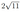
B основании прямой треугольной призмы \(A B C A_1 B_1 C_1\) лежит равнобедренный (\(A B=B C\)) треугольник \(A B C\). Точка \(K\) — середина ребра \(A_1 B_1\), а точка \(M\) делит ребро \(A C\) в отношении \(A M: M C=1: 3\).

а) Докажите, что \(K M \perp A C\).

б) Найдите угол между прямой \(K M\) и плоскостью \(A B B_1\), если \(A B=6, A C=8\) и \(A A_1=3\).

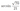
В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит параллелограмм \(A B C D\) с углом \(60^{\circ}\) при вершине \(A\). На рёбрах \(A_1 B_1, B_1 C_1\) и \(B C\) отмечены точки \(M, K\) и \(N\) соответственно так, что четырёхугольник \(A M K N\) — равнобедренная трапеция с основаниями 1 и 2.

а) Докажите, что точка \(M\) — середина ребра \(A_1 B_1\).

б) Найдите высоту призмы, если её объём равен 5 и известно, что точка \(K\) делит ребро \(B_1 C_1\) в отношении \(B_1 K: K C_1=2: 3\).

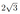
Дана правильная четырёхугольная призма \(A B C D A_1 B_1 C_1 D_1\). Плоскость \(\alpha\) проходит через вершины \(B_1\) и \(D\) и пересекает рёбра \(A A_1\) и \(C C_1\) в точках \(M\) и \(K\) соответственно. Известно, что четырёхугольник \(M B_1 K D\) — ромб.

а) Докажите, что точка \(M\) — середина рёбра \(A A_1\).

б) Найдите высоту призмы \(A B C D A_1 B_1 C_1 D_1\), если площадь её основания \(A B C D\) равна 3, а площадь ромба \(M B_1 K D\) равна 6.

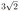
В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит равнобедренная трапеция \(A B C D\) с основаниями \(A D=3\) и \(B C=2\). Точка \(M\) делит ребро \(A_1 D_1\) в отношении \(A_1 M: M D_1=1: 2\), а точка \(K\) — середина ребра \(D D_1\).

а) Докажите, что плоскость \(M K C\) параллельна прямой \(B D\).

б) Найдите тангенс угла между плоскостью \(M K C\) и плоскостью основания призмы, если \(\angle M K C=90^{\circ}, \angle A D C=60^{\circ}\).

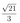
В правильной треугольной призма \(A B C A_1 B_1 C_1\) сторона \(A B\) основания равна 6, а боковое ребро \(A A_1\) равно 4. На рёбрах \(A A_1\) и \(B B_1\) отмечены точки \(M\) и \(N\) соответственно, причём \(A M=B N=3\).

а) Точки \(O\) и \(O_1\) — центры окружностей, описанных около треугольников \(A B C\) и \(A_1 B_1 C_1\) соответственно. Докажите, что прямой \(O O_1\) содержит точку пересечения медиан треугольника \(C M N\).

б) Найдите расстояние от точки \(C_1\) до плоскости \(C M N\).

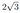
В основании прямой призмы \(A B C A_1 B_1 C_1\) лежит равнобедренный треугольник \(A B C\) с основанием \(A B\). Точка \(P\) делит ребро \(A B\) в отношении \(A P: P B=1: 3\), а точка \(Q\) — середина ребра \(A_1 C_1\). Через середину \(M\) ребра \(B C\) провели плоскость \(\alpha\), перпендикулярную отрезку \(P Q\).

а) Докажите, что плоскость \(\alpha\) параллельна ребру \(A B\).

б) Найдите отношение, в котором плоскость \(\alpha\) делит отрезок \(P Q\), считая от точки \(P\), если известно, что \(A B=A A_1, A B: B C=2: 5\).

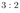
В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит параллелограмм \(A B C D\). На рёбрах \(A_1 B_1\), \(B_1 C_1\) и \(B C\) отмечены точки \(M, K\) и \(N\) соответственно, причём \(B_1 K: K C_1=1: 2\). Четырёхугольник \(A M K N\) — равнобедренная трапеция с основаниями 2 и 3.

а) Докажите, что точка \(N\) — середина ребра \(B C\).

б) Найдите площадь трапеции \(A M K N\), если объём призмы равен 12, а высота призмы равна 2.

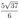
В основании прямой призмы \(A B C D A_1 B_1 C_1 D_1\) лежит равнобедренная трапеция \(A B C D\) с основаниями \(A D=3\) и \(B C=2\). Точка \(M\) делит ребро \(A_1 D_1\) в отношении \(A_1 M: M D_1=1: 2\), а точка \(K\) — середина ребра \(D D_1\).

а) Докажите, что плоскость \(M K C\) делит отрезок \(B B_1\) пополам.

б) Найдите площадь сечения призмы плоскостью \(M K C\), если \(\angle M K C=90^{\circ}, \angle A D C=60^{\circ}\).

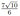
В основании прямой призмы \(A B C A_1 B_1 C_1\) лежит равнобедренный треугольник \(A B C\) с основанием \(A B\). Точка \(P\) делит ребро \(A B\) в отношении \(A P: P B=1: 3\), а точка \(Q\) — середина ребра \(A_1 C_1\). Через середину \(M\) ребра \(B C\) провели плоскость \(\alpha\), перпендикулярную отрезку \(P Q\).

а) Докажите, что плоскость \(\alpha\) делит ребро \(A C\) пополам.

б) Найдите отношение, в котором плоскость \(\alpha\) делит ребро \(A_1 C_1\), считая от точки \(A_1\), если известно, что \(A B=A A_1, A B: B C=2: 5\).

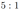
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A, B\) и \(C\), а на окружности другого основания — точка \(C_1\), причём \(C C_1\) — образующая цилиндра, а \(A C\) — диаметр основания. Известно, что \(\angle A C B=45^{\circ}, A B=2 \sqrt{3}, C C_1=2 \sqrt{6}\).

а) Докажите, что угол между прямыми \(A C_1\) и \(B C\) равен \(60^{\circ}\).

б) Найдите расстояние от точки \(B\) до прямой \(A C_1\).

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A\) и \(B\), а на окружности другого основания — точки \(B_1\) и \(C_1\), причём \(B B_1\) — образующая цилиндра, а отрезок \(A C_1\) пересекает ось цилиндра.

а) Докажите, что угол \(A B C_1\) прямой.

б) Найдите площадь боковой поверхности цилиндра, если \(A B=20, B B_1=15, B_1 C_1=21\).

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A\) и \(B\), на окружности другого основания — точки \(B_1\) и \(C_1\), причём \(BB_1\) — образующая цилиндра, а отрезок \(AC_1\) пересекает ось цилиндра.

а) Докажите, что угол \(ABC_1\) прямой.

б) Найдите угол между прямыми \(BB_1\) и \(AC_1\), если \(AB=10\), \(BB_1=7\), \(B_1C_1=24\).

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A, B\) и \(C\), а на окружности другого основания — точка \(C_1\), причём \(CC_1\) — образующая цилиндра, а \(AC\) — диаметр основания. Известно, что \(\angle ACB=30^{\circ}, AB=\sqrt{2}, CC_1=2\).

а) Докажите, что угол между прямыми \(AC_1\) и \(BC\) равен \(45^{\circ}\).

б) Найдите объём цилиндра.

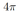
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A, B\) и \(C\), а на окружности другого основания — точка \(C_1\), причём \(C C_1\) — образующая цилиндра, а \(A C\) — диаметр основания. Известно, что \(\angle A C B=30^{\circ}, A B=1, C C_1=2 \sqrt{2}\).

а) Докажите, что угол между прямыми \(A C_1\) и \(B C\) равен \(60^{\circ}\).

б) Найдите площадь боковой поверхности цилиндра.

В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A\) и \(B\), а на окружности другого основания — точки \(B_1\) и \(C_1\), причём \(B B_1\) — образующая цилиндра, а отрезок \(A C_1\) пересекает ось цилиндра.

а) Докажите, что угол \(A B C_1\) прямой.

б) Найдите угол между прямыми \(B B_1\) и \(A C_1\), если \(A B=6, B B_1=15, B_1 C_1=8\).

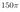
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A\) и \(B\), а на окружности другого основания — точки \(B_1\) и \(C_1\), причём \(B B_1\) — образующая цилиндра, а отрезок \(A C_1\) пересекает ось цилиндра.

а) Докажите, что угол \(A B C_1\) прямой.

б) Найдите расстояние от точки \(B\) до прямой \(A C_1\), если \(A B=21, B B_1=12, B_1 C_1=16\).

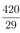
Различные точки \(A, B\) и \(C\) лежат на окружности основания конуса с вершиной \(S\) так, что отрезок \(A B\) является её диаметром. Угол между образующей конуса и плоскостью основания равен \(60^{\circ}\).

а) Докажите, что \(\cos \angle A S C+\cos \angle B S C=1,5\).

б) Найдите объём тетраэдра \(S A B C\), если \(S C=1, \cos \angle A S C=\frac{2}{3}\).

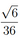
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки \(A\) и \(B\), а на окружности другого основания — точки \(B_1\) и \(C_1\), причём \(B B_1\) — образующая цилиндра, а отрезок \(A C_1\) пересекает ось цилиндра.

а) Докажите, что угол \(ABC_1\) прямой.

б) Найдите объём цилиндра, если \(AB=7, BB_1=24, B_1 C_1=10\).