Начать бесплатно
Войти
Подготовка к ЕГЭ
Бесплатные материалы
Сотрудничество
О нас
Преподаватели
Начать бесплатно
Войти
Подготовка к ЕГЭ
Бесплатные материалы
Сотрудничество
О нас
Преподаватели
Зарегистрироваться
Начать бесплатно
Войти
Написать в ЛС
Активировать промокод

Уравнения

ЕГЭ 2023

Telegram основной
ВКонтакте
ВКонтакте
Telegram основной
Другие бесплатные материалы от Профиматики
Банк 1 части ЕГЭ
Ященко 2025
Банк ФИПИ
Полезные материалы
Telegram для преподавателей
⬈
Наши соцсети:
Хочешь больше полезных материалов? Переходи по ссылкам
Задание 1
Katex

а) Решите уравнение

\(\log _3\left(\cos{\left(\dfrac{\pi}{2}-x\right)}+\sin{2x} +81\right)=4.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-\dfrac{7\pi}{2};-2\pi\right]\)

Показать ответ и решение
+
Ответ:
Задание 2
Katex

а) Решите уравнение

\(27^x-10\cdot3^{x+1}+\dfrac{81}{3^x}=0.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\log_7{2};\log_7{15}\right]\)

Показать ответ и решение
+
Ответ:
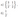
Задание 3
Katex

а) Решите уравнение

\(2\cos^3{x} = \sqrt{3}\sin^2{x}+2\cos{x}.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-3\pi;-\dfrac{5\pi}{2}\right]\)

Показать ответ и решение
+
Ответ:
Готовься с нами на курсе
Пока ты откладываешь, другие уже набирают 90+ баллов. А ты?
Задание 4
Katex

а) Решите уравнение

\(\sin{x}\cos{2x}-\sqrt{2}\cos^2{x} + \sin{x}=0.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)

Показать ответ и решение
+
Ответ:
Задание 5
Katex

а) Решите уравнение

\(2\sin^2{x}\cos{x}+\sqrt{3}\cos^2{x}=\sqrt{3}.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{5\pi}{2};4\pi\right]\)

Показать ответ и решение
+
Ответ:
Задание 6
Katex

а) Решите уравнение

\(\log_3{x}\cdot\log_3{\left(4x^2-1\right)} = \log_3\dfrac{x(4x^2-1)}{3}.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\log_5{2};\log_5{27}\right]\)

Показать ответ и решение
+
Ответ:
Задание 7
Katex

а) Решите уравнение

\(\sin{2x}=\sin{x} - 2\sin{\left(x-\dfrac{3\pi}{2}\right) +1}.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[\dfrac{3\pi}{2};3\pi\right]\)

Показать ответ и решение
+
Ответ:
Задание 8
Katex

а) Решите уравнение

\(\sin{2x} + 2\cos{\left(x-\dfrac{\pi}{2}\right)} = \sqrt{3}\cos{x} + \sqrt{3}.\)


б) Найдите все корни этого уравнения, принадлежащие отрезку \(\left[-3\pi;-\dfrac{3\pi}{2}\right]\)

Показать ответ и решение
+
Ответ:
⚡️ протестируй свой уровень
⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ
Бесплатный пробный урок любого курса