



Планиметрия
Прямоугольный
треугольник
▶ 1. Напротив угла в \(30^{\circ}\) лежит катет, равный половине гипотенузы: если \(\alpha=30^{\circ}\), тогда \(2a=c\).
Замечание: Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то напротив этого катета угол \(30^{\circ}\).
Замечание: Если сторона напротив угла \(30^{\circ}\) вдвое меньше прилежащей к углу стороне, то треугольник прямоугольный (это не школьная теорема).
▶ 2. Теорема Пифагора: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
▶ 3. Медиана, проведённая к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Верно и обратное: если в треугольнике одна из медиан равна половине стороны, к которой она проведена, то эта медиана исходит из вершины прямого угла. То есть наш треугольник - прямоугольный.
▶ 4. Гипотенуза является диаметром, а ее середина - центром окружности, описанной вокруг данного прямоугольного треугольника.
▶ 5. Гипотенуза является диаметром, а ее середина - центром окружности, описанной вокруг данного прямоугольного треугольника.
▶ 6. Высота прямоугольного треугольника, опущенная на гипотенузу, вычисляется по формуле:
▶ 7. Пусть \(x_a\), \(x_b\), \(x_c\) - соответственные линейные элементы прямоугольных треугольников с гипотенузами \(a\), \(b\), \(c\) соответственно, тогда
▶ 8. В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен разности острых углов треугольника.
▶ 9. Радиус вписанной в прямоугольный треугольник окружности равен
▶ 10. В прямоугольном треугольнике биссектриса прямого угла является также биссектрисой треугольника, образованного высотой, медианой (которые проведены из вершины прямого угла) и отрезком гипотенузы.
Верно и обратное: если в треугольнике биссектриса делит пополам угол между высотой и медианой, исходящими из того же угла, то такой треугольник является прямоугольным.
Замечание: Обратите внимание, что это могут быть как отдельные соответственные элементы, так и их линейные комбинации: \(I_a\), \(I_b\), \(I_c\) (центры ); \(p_a\), \(p_b\), \(p_c\); \(r_a + R_a\), \(r_b + R_b\), \(r_c + R_c\) и т.д.
Например, пусть \(p_a\), \(p_b\), \(p_c\) - полупериметры соответственно треугольников \(CBH\), \(ACH\), \(ABC\), тогда \(p^2_a + p^2_b = p^2_c.\)
Если \(r_a\), \(r_b\), \(r_c\) - радиусы вписанных окружностей, \(R_a, R_b, R_c\) - радиусы описанных окружностей треугольников \(CBH\), \(ACH\), \(ABC\), тогда \((r_a + R_a)^2 + (r_b + R_b)^2 = (r_c + R_c)^2\).










Доказательство:
Отложим от точки \(C\) отрезок \(B'C\), такой что \(B'C = BC = a\), и точки \(B\), \(C\), \(B'\) - лежат на одной прямой. Тогда в треугольнике \(ABB'\) \(AC\) - высота и медиана, значит, \(ABB'\) - равнобедренный треугольник (\(\angle{B'} = \angle{B}\)). \(AC\) - биссектриса угла \(\angle{B'AB}\), поэтому \(\angle{B'AB} = 60^{\circ}\), отсюда следует, что оставшиеся углы треугольника также равны \(60^{\circ}\), то есть \(ABB'\) - равносторонний треугольник, в частности \(2a = BB' = AB = c\).
\(\Box\)
Замечание: Пусть в треугольнике \(ABC\) \(\angle{CAB} = 30^{\circ}\), \(BC = a\), \(AB = 2a\), \(AC = b\). Воспользуемся теоремой косинусов:
\(
a^2 = (2a)^2 + b^2 - 2ab\cos{30^{\circ}}\Longleftrightarrow b^2 - 2\sqrt{3}ab + 3a^2 = 0\Longleftrightarrow (b - a\sqrt{3})^2 = 0\Longleftrightarrow b = a\sqrt{3}.
\)
Заметим, что для треугольника со сторонами \(a\), \(\sqrt{3}a\), \(2a\) верна теорема Пифагора:
\(
a^2 + (\sqrt{3}a)^2 = 4a^2 = (2a)^2.
\)
Значит \(ABC\) - прямоугольный треугольник.

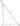
Доказательство:
Достроим треугольник \(ABC\) до квадрата \(CHFD\) со стороной \((a+b)\) как показано на рисунке. Треугольники \(ABC\), \(GAH\), \(EGF\), \(BED\) равны по двум сторонам (катетам) и углу между ними. \(\alpha + \beta = 90^{\circ}\), поэтому \(AGEB\) - квадрат. Таким образом, площадь квадрата \(CHFD\) равна, с одной стороны \((a + b)^2\), с другой стороны \(4\cdot\dfrac{ab}{2} + c^2\), то есть
\((a + b)^2 = 2ab + c^2\;\;\;\Longrightarrow\;\;\; a^2 + 2ab + b^2 = 2ab + c^2\;\;\;\Longrightarrow\;\;\;a^2 + b^2 = c^2.\)
Докажем обратное утверждение. Пусть в треугольнике \(ABC\) со сторонами \(CB = a\), \(AC = b\), \(AB = c\) выполнено равенство верно \(a^2 + b^2 = c^2\). Рассмотрим прямоугольный треугольник \(A_1B_1C_1\), так что \(C_1B_1 = a\), \(A_1C_1 = b\). По теореме Пифагора \(A_1B_1^2 = a^2 + b^2 = AB^2 = c^2\), то есть \(A_1B_1 = AB = c\), значит треугольники \(ABC\), \(A_1B_1C_1\) равны по трём сторонам, значит \(ABC\) - прямоугольный.
\(\Box\)

Доказательство:
Продлим медиану \(CM\) на её длину до точки \(D\), то есть \(CM = MD\). Треугольники \(CMB\) и \(MDA\) равны по двум сторонам и углу между ними (\(CM = MD\), \(BM = MA\), \(\angle{CMB} = \angle{AMD}\), так как они являются вертикальными), значит, \(\angle{CBM} = \angle{MAD}\). Аналогично, подобны треугольники \(CAM\) и \(DBM\), а, значит, \(\angle{CAM} = \angle{MBD}\). Таким образом, треугольники \(ABC\) и \(BAD\) равны, значит \(CADB\) - прямоугольник, в котором \(AB\) и \(CD\) - диагонали, они равны и точкой пересечения делятся пополам, поэтому
Докажем обратное утверждение: опишем вокруг треугольника \(ABC\) окружность. Нам известно, что \(CM = AM = MB\), поэтому радиус описанной окружности равен \(AM\) и \(M\) - центр окружности, \(AB\) - диаметр окружности, угол \(\angle{ACB}\) равен \(90^{\circ}\), так как он опирается на диаметр окружности, значит, наш треугольник является прямоугольным.
\(\Box\)
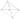

Доказательство:
\(\angle{HCB} = 180^{\circ} - (90^{\circ} + \beta) = 90^{\circ} - \beta = \alpha\), значит треугольники \(ABC\) и \(CBH\) подобны по трём углам. Аналогично, \(\angle{ACH} = 180^{\circ} - (90^{\circ} + \alpha) = 90^{\circ} - \alpha = \beta\), то есть треугольники \(ABC\) и \(ACH\) подобны.
Из подобия этих двух пар треугольников следует, что треугольники \(AHC\) и \(CHB\) подобны.
\(\Box\)
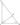
Доказательство:
Так как треугольники \(ABC\) и \(ACH\) подобны, то мы можем записать соотношение:
\(\dfrac{CH}{CB} = \dfrac{AC}{AB}\;\;\;\text{или}\;\;\;\dfrac{h}{a} = \dfrac{b}{c}\;\;\;\Longrightarrow h = \dfrac{ab}{c}.\)
А также:
\(\dfrac{AC}{AB} = \dfrac{AH}{AC}\;\;\;\text{или}\;\;\;\dfrac{b}{c} = \dfrac{c_b}{b}\;\;\;\Longrightarrow c_bc=b^2.\)
Из подобия треугольников \(ACH\) и \(CBH\) получаем:
\(\dfrac{CH}{AH} = \dfrac{HB}{CH}\;\;\;\text{или}\;\;\;\dfrac{h}{c_b} = \dfrac{c_a}{h}\;\;\;\Longrightarrow h^2 = c_ac_b.\)
Из подобия \(ABC\) и \(CBH\) следует:
\(\dfrac{CB}{AB} = \dfrac{HB}{CB}\;\;\;\text{или}\;\;\;\dfrac{a}{c} = \dfrac{c_a}{a}\Longrightarrow c_ac=a^2.\)
\(\Box\)
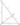
Доказательство:
В подобных треугольниках линейные элементы относятся также как стороны этих треугольников. Поэтому для треугольников \(ABC\) и \(CBH\) получаем:
\(\dfrac{a}{c} = \dfrac{x_a}{x_c}.\)
Для треугольников \(ABC\) и \(ACH\):
\(\dfrac{b}{c} = \dfrac{x_b}{x_c}.\)
Возведём в квадрат оба равенства и сложим:
\(\dfrac{a^2 + b^2}{c^2} = \dfrac{x^2_a + x^2_b}{x^2_c}.\)
\(\dfrac{a^2 + b^2}{c^2} = 1\), поэтому \(x^2_a + x^2_b = x^2_c\)
\(\Box\)
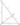
Доказательство:
Докажем данное утверждение при \(\beta > \alpha\).
\(CM\) - медиана исходящая из прямого угла, поэтому \(CM = MA\), значит \(\angle{ACM} = \angle{MAC} = \alpha\). Мы знаем, что
\(\alpha + \beta = 90^{\circ}.\) Треугольник \(HCB\) прямоугольный, поэтому \(\angle{HCB} + \angle{HBC} = 90^{\circ}\), то есть \(\angle{HCB} = 90^{\circ} - \beta = \alpha\). С одной стороны, \(\angle{MCH} + 2\alpha = 90^{\circ}\), с другой \(\alpha + \beta = 90^{\circ}\), значит,
\(\angle{MCH} + 2\alpha = \alpha + \beta\)
То есть \(\angle{MCH} = \beta - \alpha.\)
\(\Box\)
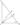
Доказательство:
\(B'C = CA' = r\), \(A'B = BC' = a-r\), \(B'A = AC' = b-r\), значит,
\(\Box\)

Доказательство:
\(CM\) - медиана исходящая из прямого угла, поэтому \(CM = MB\), значит, \(\angle{MBC} = \angle{MCB}\). \(ABC\) - прямоугольный, поэтому \(\angle{CAB} + \angle{MBC} = 90^{\circ}\), \(ACH\) также является прямоугольным, поэтому
\(\Box\)

⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ









