



Планиметрия
Треугольники
общего вида
Сумма внутренних углов треугольника равна \(180^{\circ}\).

▶ 1. Первый признак равенства треугольников: по двум сторонам и углу между ними. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

▶ 2. Второй признак равенства треугольников: по стороне и прилежащим к ней углам. Если сторона и прилежащие к ней углы равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Замечание: На самом деле ситуация, в которой один угол прилёг к стороне, а второй - нет, также приводит к равенству треугольников, так как оставшийся угол задаётся однозначно по двум известным.
Ситуация, в которой одна из пар равных углов прилегает к равной стороне, а вторая пара равных углов нет, тоже приводит к равенству треугольников. Действительно, пусть нам даны треугольники \(ABC\) и \(A_1B_1C_1\), причём \(\angle{A} = \angle{A_1}\), \(\angle{B} = \angle{B_1}\), \(AC = A_1C_1\), тогда

▶ 3. Третий признак равенства треугольников: по трем сторонам. Если три стороны треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.

▶ 4. Если две стороны и угол напротив одной из сторон первого треугольника соответственно равны двум сторонам и углу второго треугольника, то возможны два варианта:
1) Углы напротив второй стороны равны \(\Longleftrightarrow\) треугольники равны

2) Углы напротив второй стороны дополняют друг друга до \(180^{\circ}\) \(\Longleftrightarrow\) треугольники не равны (кроме случая прямоугольного треугольника).

Замечание:
Покажем, почему в четвёртом признаке равенства треугольников возникает два случая. Пусть длина стороны \(AB\) равна \(a\), длина стороны \(BC\) равна \(b\) и угол при вершине \(C\) равен \(\alpha\). Построим два разных треугольника со сторонами \(a\), \(b\) и углом \(\alpha\): построим угол \(\alpha\) и назовем его вершину \(C\), от вершины \(C\) отложим на одной из сторон угла отрезок, равный по длине \(b\), его концом назовём точку \(B\), через вершину \(B\) проведём окружность радиуса \(a\), которая может пересечь вторую сторону угла в двух точках (назовём их \(A\) и \(A'\)). Тогда отрезки \(AB\) и \(A'B\) имеют длину \(a\), то есть мы получили два не совпадающих треугольника \(ABC\) и \(A'BC\), которые имеют стороны \(a\), \(b\) и угол \(\alpha\). Именно поэтому в первом признаке равенства треугольников речь идёт об угле между сторонами.

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого треугольника. Число \(k\) равное отношению соответственных сторон подобных треугольников называется коэффициентом подобия.

▶ 1. Первый признак подобия двух треугольников: по двум углам. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

▶ 2. Второй признак подобия двух треугольников: по двум пропорциональным сторонам и углу между ними. Если две стороны одного треугольника пропорциональны соответственно двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

▶ 3. Третий признак подобия двух треугольников: по трём пропорциональным сторонам. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.

▶ 4. Площади подобных треугольников относятся как квадрат коэффициента подобия.

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

▶ 1. Напротив большей стороны треугольника лежит больший угол: если \(b > a\) и \(b > c\), то \(\beta\) - больший угол треугольника.
▶ 2. Неравенство треугольника: сумма двух любых сторон треугольника всегда больше третьей стороны, то есть:

Теорема синусов:

Замечание 1: Чаще всего мы используем теорему синусов для нахождения радиуса описанной окружности.
Замечание 2: А еще мы используем теорему синусов, если знаем в треугольнике два угла и одну сторону и хотим найти еще одну сторону.


Доказательство:
Докажем, что \(2R = \dfrac{b}{\sin{\beta}}\). Оставшиеся соотношения доказываются аналогично.
Случай 1: \(\beta \leqslant 90^{\circ}\). Рассмотрим треугольник \(AB'C\), вписанный в окружность, причём \(AB'\) - диаметр окружности. Угол \(\angle{ACB'}\) опирается на диаметр окружности, поэтому он равен \(90^{\circ}\). Углы \(\angle{ABC}\) и \(\angle{AB'C}\) опираются на дугу \(\stackrel{\smile}{AC}\), значит \(\angle{AB'C} = \beta\). Отсюда получаем, что \(\sin{\beta} = \dfrac{b}{2R}\;\Longrightarrow\; 2R = \dfrac{b}{\sin{\beta}}\).
Случай 2: \(\beta > 90^{\circ}\). Рассмотрим треугольник \(ADC\), вписанный в окружность, угол \(\angle{ADC}\) опирается на дугу \(\stackrel{\smile}{CA}\), значит \(\angle{ADC} = 180^{\circ}-\beta < 90^{\circ}\), поэтому верно соотношение \(\sin{(180^{\circ} - \beta)} = \dfrac{b}{2R}\). Так как \(\sin{(180^{\circ} - \beta)} = \sin{\beta}\), имеем \(2R = \dfrac{b}{\sin{\beta}}\).
\(\Box\)
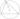
Теорема косинусов
В произвольном треугольнике верны соотношения:

Теорема косинусов позволяет:
1) Найти одну из сторон треугольника, если известны две другие стороны и угол между ними: \(a = \sqrt{b^2+c^2-2bc\cos\alpha}\).
2) Найти угол треугольника, если известны все стороны треугольника. \(\cos\alpha = \dfrac{b^2+c^2-a^2}{2bc}\).
3) Найти одну из сторон треугольника, если известные две стороны и угол не между ними из квадратного уравнения (в этом случае решений может быть два): \(a^2 - 2ac\cos\beta + c^2-b^2 = 0\) (в данном случае мы знаем стороны \(b\), \(c\) и угол между сторонами \(a\) и \(c\)).
Замечание: Теорема Пифагора - это частный случай теоремы косинусов, действительно, если \(c\) - гипотенуза, \(a\), \(b\) - катеты, получаем \(c^2 = a^2 + b^2 - 2ab\cos{90^{\circ}} = a^2 + b^2\), так как \(\cos{90^{\circ
}} = 0\).
Пусть \(c\) - большая сторона треугольника, тогда
1) если \(c^2 > a^2 + b^2\), то \(\cos{\gamma} < 0\), значит треугольник тупоугольный;
2) если \(c^2 = a^2 + b^2\), то \(\cos{\gamma} = 0\) треугольник прямоугольный;
3) если \(c^2 < a^2 + b^2\), то \(\cos{\gamma} > 0\), значит угол \(\gamma\) - острый. Так как \(\gamma\) лежит напротив большей стороны, то \(\gamma\) самый большой угол в треугольнике, а значит треугольник остроугольный.
Доказательство:
Докажем первую из формул. Остальные доказываются аналогично.
Случай 1:
Пусть углы при основании \(AC\) являются острыми. В этом случае высота \(BD\) упадёт на отрезок \(AC\). Получаем: \(\cos{\alpha} = \dfrac{AD}{c}\;\Longrightarrow\; AD = c\cdot\cos{\alpha}\), \(DC = b - c\cdot\cos{\alpha}\). Воспользуемся теоремой Пифагора для треугольников \(ABD\) и \(DBC\):

Случай 2: Пусть угол \(\alpha\) - тупой.
В этом случае высота \(BD\) упадёт на продолжение стороны \(AC\). Угол \(\angle{BAD}\) равен \(180^{\circ} - \alpha\). \(\cos{\alpha} = -\cos{180^{\circ} - \alpha}\), поэтому \(AD = -c\cdot\cos{\alpha}\), \(DC = b - c\cdot\cos{\alpha}\). Воспользуемся теоремой Пифагора для треугольников \(ABD\) и \(DBC\):

Случай 3: Пусть угол \(\gamma\) - тупой. В этом случае высота \(BD\) упадёт на продолжение стороны \(AC\). \(AD = c\cdot\cos{\alpha}\), \(CD = b - c\cdot\cos{\alpha}\). Воспользуемся теоремой Пифагора для треугольников \(ABD\) и \(DBC\):
\(\Box\)

Теорема Менелая. Пусть прямая пересекает треугольник \(ABC\), причем \(C'\) - это точка ее пересечения со стороной \(AB\), \(A'\) - точка ее пересечения со стороной \(BC\) и \(B'\) - точка ее пересечения с продолжением стороны \(AC\). Тогда имеет место соотношение:
Обратно, пусть точки \(A'\), \(B'\), \(C'\) лежат на сторонах треугольника или на их продолжениях, тогда если верно соотношение
то точки \(A'\), \(B'\), \(C'\) лежат на одной прямой.

Обратно, пусть точки \(A'\), \(B'\), \(C'\) лежат на сторонах треугольника или на их продолжениях, тогда если верно соотношение
Замечание 1. Теорему очень легко запомнить, используя следующее мнемоническое правило: «Вершина \(\rightarrow\) точка; точка \(\rightarrow\) вершина», т.е. вначале мы выбираем стартовую вершину (в нашем случае это вершина \(A\)) и идем из нее в точку пересечения прямой и стороны треугольника, выходящей из вершины \(A\) (в нашем случае в \(C'\)), из нее во вторую вершину треугольника на этой стороне (в нашем случае \(B\)) и т.д.
Замечание 2. Если бы из \(A\) мы пошли в \(B'\), ничего бы не изменилось. Наша теорема выглядела бы так:
Доказательство:
Докажем основное утверждение: через вершину \(B\) проведём прямую, параллельную стороне \(AC\), \(D\) - точка пересечения прямой \(B'C'\) с данной прямой. Углы \(\angle{AC'B'}\) и \(\angle{DC'B}\) являются вертикальными, поэтому они равны. Углы \(\angle{BAB'}\) и \(\angle{ABD}\) равны, так как являются накрест лежащими при параллельных прямых \(AB'\) и \(BD\), значит треугольники \(DC'B\) и \(B'C'A\) подобны, то есть верно соотношение \(\dfrac{B'A}{DB} = \dfrac{AC'}{C'B}.\)

Аналогично легко показать, что треугольники \(DA'B\) и \(B'A'C\) подобны, а значит выполнено соотношение \(\dfrac{DB}{CB'} = \dfrac{BA'}{A'C}.\)

Перемножим полученные равенства:
\(\dfrac{B'A}{DB}\cdot \dfrac{DB}{CB'} = \dfrac{AC'}{C'B}\cdot \dfrac{BA'}{A'C}\;\;\;\Longrightarrow\;\;\;\dfrac{B'A}{CB'} = \dfrac{AC'\cdot BA'}{C'B\cdot A'C}\;\;\;\Longrightarrow\;\;\;\dfrac{AC'}{C'B}\cdot\dfrac{BA'}{A'C}\cdot\dfrac{CB'}{B'A} = 1.\)
\(\Box\)
Докажем обратное утверждение.
Пусть выполнено соотношение
Отсюда получаем, что
\(\dfrac{BA''}{A''C} = \dfrac{BA'}{A'C} = \dfrac{BA''}{AC - BA''} = \dfrac{BA'}{AC - BA'}\;\;\;\Longrightarrow\;\;\;BA''\cdot AC - BA''\cdot BA' = BA'\cdot AC - BA''\cdot BA'\)
\(\Longrightarrow\;\;\;BA''\cdot AC = BA'\cdot AC\;\;\;\Longrightarrow\;\;\;BA'' = BA',\)
значит точки \(A'\) и \(A''\) совпадают, поэтому точки \(A'\), \(B'\), \(C'\) лежат на одной прямой.
\(\Box\)

Чевианой будем называть любой отрезок, соединяющий вершину треугольника с противоположной стороной.
Теорема Чевы. Если три чевианы \(AA'\), \(BB'\), \(CC'\), проведённые из разных вершин треугольника, пересекаются в одной точке, то выполнено соотношение:
Обратно, если выполнено соотношение
то чевианы пересекаются в одной точке.

Замечание. Теорему Чевы можно запомнить ровно так же, как и теорему Менелая: то есть вначале мы выбираем стартовую вершину (в нашем случае это вершина \(A\)) и идем из нее в точку пересечения чевианы и стороны треугольника, выходящей из вершины \(A\) (в нашем случае в \(C'\)), из нее во вторую вершину треугольника на этой стороне (в нашем случае \(B\)) и т.д.
Прямая, перпендикулярная данному отрезку и проходящая через его середину, называется серединным перпендикуляром.
Доказательство:
Докажем прямую теорему Чевы. Применим теорему Менелая для треугольника \(ABB'\) и прямой \(CC'\):

Перемножим полученные равенства:
\(\dfrac{AC'}{C'B}\cdot\dfrac{BA'}{A'C}\cdot\dfrac{BK}{KB'}\cdot\dfrac{CA}{AB'}\cdot\dfrac{B'C}{CA}\cdot\dfrac{B'K}{KB} = 1.\)
Отсюда получаем:
Докажем обратное утвержедние. Прямые \(AA'\) и \(CC'\) пересекаются в точке \(K\). Пусть прямая \(BK\) пересекает \(AC\) в точке \(B''\). Тогда по прямой теореме Чевы получаем:
При этом верно равенство
\(\Box\)

Прямая, перпендикулярная данному отрезку и проходящая через его середину, называется серединным перпендикуляром.
▶ 1. Если точка равноудалена от концов отрезка, то она лежит на его серединном перпендикуляре.
Обратно, если точка лежит на серединном перпендикуляре к некоторому отрезку, то она равноудалена от концов этого отрезка.

▶ 2. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром описанной вокруг треугольника окружности.


Доказательство:
Пусть точка \(B\) равноудалена от точек \(A\) и \(C\), то есть \(AB = BC\). Пусть \(M\) - середина отрезка \(AC\), то есть \(AM = MC\). Сторона \(BM\) общая для треугольников \(ABM\) и \(CBM\), значит эти треугольники равны по трём сторонам. Значит \(\angle{AMB} = \angle{CMB}\), при этом они являются смежными, а значит в сумме дают \(180^{\circ}\), поэтому они оба равны \(90^{\circ}\).
\(\Box\)
Докажем обратное утверждение. Пусть точка \(B\) лежит на серединном перпендикуляре. \(AM = MC\) и сторона \(BM\) общая для треугольников \(ABM\) и \(CBM\), а значит прямоугольные треугольники \(ABM\) и \(CBM\) равны, следовательно равны их гипотенузы: \(AB = AC\).
\(\Box\)

Доказательство:
Пусть серединные перпендикуляры к сторонам \(AC\) и \(BC\) пересекаются в точке \(O\). Тогда по свойству серединного перпендикуляра получаем: \(AO = OC\) и \(AO = OB\), то есть \(OB = OC\), следовательно точка \(O\) лежит на серединном перпендикуляре к стороне \(BC\), значит \(O\) - точка пересечения серединных перпендикуляров. \(AO = OB = OC\), поэтому центр описанной окружности лежит в точке \(O\).
\(\Box\)

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит каждую из них в отношении \(2:1\), считая от вершины треугольника.

Замечание. Данный факт также можно доказать при помощи теоремы Менелая. Возьмём треугольник \(ABB'\) и прямую \(CC'\), тогда по теореме Менелая получим:
\(\dfrac{AC'}{C'B}\cdot\dfrac{BM}{MB'}\cdot\dfrac{B'C}{CA} = 1\;\Longrightarrow\; \dfrac{BM}{MB'}\cdot\dfrac{1}{2} = 1\;\Longrightarrow \dfrac{BM}{MB'} = 2.\)
Доказательство:
Докажем, что
\(\Box\)
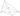
Биссектрисой называется луч, исходящий из вершины угла и делящий этот угол на два равных угла.
Биссектрисой треугольника называют отрезок биссектрисы одного из углов треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

▶ 1. Точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Обратно, точка, равноудалённая от сторон угла, лежит на биссектрисе этого угла.
▶ 2. Биссектрисы треугольника пересекаются в одной точке, которая является центром вписанной в треугольник окружности.


Доказательство:
Пусть \(D\) - точка, лежащая на биссектрисе. Опустим из неё перпендикуляры на стороны угла. Получим два прямоугольных треугольника: \(ABD\) и \(ACD\). \(AD\) - их общая сторона, \(\angle{BAD} = \angle{DAC}\), значит треугольники \(ABD\) и \(ACD\) равны и \(BD = DC\).
\(\Box\)
Докажем обратное утверждение. Пусть \(D\) равноудалена от сторон угла \(A\), тогда у прямоугольных треугольников \(ABD\) и \(ACD\) есть общая сторона \(AD\) и равные стороны \(BD\) и \(DC\), значит треугольники равны, поэтому \(\angle{BAD} = \angle{DAC}\), то есть \(AD\) - биссектриса.
\(\Box\)
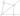
Доказательство:
Пусть \(I\) - точка пересечения биссектрис углов \(\angle{A}\) и \(\angle{B}\), а \(IA'\), \(IB'\), \(IC'\) - перпендикуляры к сторонам треугольника. Точка \(I\) лежит на биссектрисе угла \(A\), значит, \(IB' = IC'\), аналогично получаем, что \(IA' = IC'\), значит, \(IB' = IA'\), то есть точка \(I\) равноудалена от сторон угла \(C\), значит, она лежит на биссектрисе угла \(C\). \(IA' = IB' = IC'\), поэтому \(I\) - центр вписанной окружности.
\(\Box\)

Доказательство:
Через вершины \(A\), \(B\) и \(C\) проведём прямые, параллельные сторонам, лежащим напротив данных вершин. Пусть эти прямые пересекаются в точках \(A_1\), \(B_1\), \(C_1\). Получаем треугольник \(A_1B_1C_1\), причём высоты \(AA'\), \(BB'\), \(CC'\) треугольника \(ABC\) перпендикулярны сторонам \(C_1B_1\), \(A_1C_1\) и \(B_1A_1\) соответственно.
Рассмотрим четырёхугольник \(AC_1BC\). По построению получаем, что \(AC_1 || CB\) и \(AC || C_1B\), значит \(AC_1BC\) - параллелограмм, то есть \(BC_1 = AC\) и \(AC_1 = BC\). Аналогично получаем, что четырёхугольники \(ABA_1C\) и \(ABCB_1\) также являются параллелограммами и
\(A_1B = AC,\;\;\; A_1C = AB,\;\;\; B_1C = AB,\;\;\; AB_1 = BC,\)
следовательно,
\(C_1A = AB_1,\;\;\; C_1B = BA_1,\;\;\; A_1C = CB_1.\)
Значит отрезки \(AA'\), \(BB'\), \(CC'\) лежат на серединных перпендикулярах к сторонам треугольника \(A_1B_1C_1\). Серединные перпендикуляры пересекаются в одной точке, значит высоты треугольника \(ABC\) пересекаются в одной точке.
\(\Box\)

Калиткой будем называть отрезок, соединяющий вершину угла с точкой касания вписанной в этот угол окружности (это не устоявшийся термин, его не следует использовать на ЕГЭ).
▶ 1. Длины калиток любого угла равны.
▶ 2. Пусть дан треугольник \(ABC\), \(AB = c\), \(AC = b\), \(BC = a\) и \(p = \dfrac{a+b+c}{2}\). Тогда калитка угла \(A\) имеет длину \(p - a\), калитка угла \(B\) имеет длину \(p - b\) и калитка угла \(C\) имеет длину \(p - c\).
Окружность, которая касается стороны треугольника и продолжений двух его сторон называется вневписанной окружностью треугольника.
▶ 3. Пусть дана вневписанная окружность, касающаяся стороны \(BC\) треугольника \(ABC\). Тогда длина калитки угла \(A\) равна \(p\). длина калитки внешнего угла \(C\), равна \(p-b\); длина калитки внешнего угла \(B\), равна \(p-c\).
▶ 4. Пусть в четырёхугольник \(ABCD\) можно вписать окружность, тогда





Доказательство:
Пусть \(A\) и \(B\) - точки касания угла и вписанной в него окружности, они равноудалены от центра \(O\), значит, \(O\) лежит на биссектрисе нашего угла, отсюда следует, что прямоугольные треугольники \(ACO\) и \(BCO\) равны, а значит \(AC = CB\).
\(\Box\)
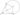
Доказательство:
Пусть \(k_{A}\) - калитка угла \(A\), \(k_{B}\) - калитка угла \(B\), \(k_{C}\) - калитка угла \(C\). Тогда \(k_{A} + k_{B} + k_{C} = p\). \(AB' + B'C = k_{A} + k_{C} = b\), значит \(k_{B} = p - b\). Аналогично, \(k_{B} + k_{C} = a\), значит \(k_{A} = p - a\); \(k_{A} + k_{B} = c\), значит \(k_{C} = p - c\).
\(\Box\)

Доказательство:
\(AB + BC + CA = a + b + c = 2p\), \(BA' = BC'\), \(A'C = CB'\), значит \(AC' + AB' = AB + BC' + AC + CB' = AB + AC + BA' + A'C = a + b + c\), причём \(AB' = AC'\), значит \(AB' = AC' = p\). \(CB' = AB' - AC = p - b\), аналогично \(BC' = AC' - BC' = p - c\).
\(\Box\)

Доказательство:
Если в четырёхугольник можно вписать окружность, то
Тогда получаем:
\(
(AP + BP) + (CR + DR) = AB + CD;\;\;\; (AS + DS) + (BQ + CQ) = AD + BC.
\)
И, значит, \(AB + CD = AD + BC\).
Докажем обратное утверждение.
Пусть в четырёхугольнике \(ABCD\) верно, что \(AB + CD = AD + BC\). Биссектрисы углов \(CBA\) и \(DAB\) пересекаются в точке \(I\). Эта точка равноудалена от сторон \(AB\), \(AD\) и \(BC\), значит \(I\) - центр окружности, касающейся сторон \(AB\), \(AD\) и \(BC\) нашего четырёхугольника. Пусть
\(CD\) не касается данной окружности Далее рассмотрим \(2\) случая.
Случай 1. Сторона \(CD\) не пересекается с окружностью. На отрезках \(BC\) и \(AD\) отметим соответственно точки \(C'\) и \(D'\) так, что \(C'D'\) - касательная к нашей окружности и \(C'D'\) не пересекает \(CD\). В четырёхугольник \(ABC'D'\) можно вписать окружность. По доказанному ранее получаем, что
\(
AB + C'D' = AD' + BC'.
\)
При этом
\(
BC' = BC - CC';\;\;\; AD' = AD - DD'.
\)
Значит,
\(
AB + C'D' = BC - CC' + AD - DD'\Longleftrightarrow C'D' + CC' + DD' = AD + BC - AB.
\)
При этом мы знаем, что \(CD = AD + BC - AB\), то есть
\(
CD = C'D' + CC' + DD'.
\)
Тогда мы получаем, что в четырёхугольнике \(CDD'C'\) одна сторона равна сумме трёх других, что невозможно. Получаем противоречие.
Случай 2. Сторона \(CD\) пересекает окружность в двух точках. Проведём касательную \(C'D'\) параллельно отрезку \(CD\). В четырёхугольник \(ABC'D'\) можно вписать окружность. По доказанному ранее получаем, что
\(
AB + C'D' = AD' + BC'.
\)
При этом
\(
BC' = BC + CC';\;\;\; AD' = AD + DD'.
\)
Значит,
\(
AB + C'D' = BC + CC' + AD + DD'\Longleftrightarrow C'D' - CC' - DD' = AD + BC - AB
\)
При этом мы знаем, что \(CD = AD + BC - AB\), то есть
\(
CD = C'D' - CC' - DD'\Longleftrightarrow C'D' = CD + CC' + DD'.
\)
Тогда мы получаем, что в четырёхугольнике \(CDD'C'\) одна сторона равна сумме трёх других, что невозможно. Получаем противоречие.

▶ 1. Теорема Фалеса Если на одной стороне угла отложить равные
отрезки и через их концы провести параллельные прямые, пересекающие вторую сторону угла, то на второй стороне угла будут высечены также равные отрезки.
▶ 2. Обратная теорема Фалеса. Если прямые, пересекающие стороны угла, отсекают на обеих из них равные между собой отрезки, начиная от вершины, то такие прямые параллельны.
▶ 3. Обобщенная теорема Фалеса. Если на одной из сторон угла последовательно отложить отрезки и через их концы провести параллельные прямые, то прямые отсекут на другой стороне угла, отрезки, пропорциональные отрезкам на первой стороне.
▶ 4. Обратная обобщённая теорема Фалеса. Если прямые, пересекающие стороны угла, отсекают на обеих из них пропорциональные между собой отрезки, начиная от вершины, то такие прямые параллельны.
Замечание: очень важно, что пропорциональные (равные) отрезки должны начинаться от вершины угла, иначе обратные теоремы не будут работать.



▶ 1. Углы при основании равнобедренного треугольника равны. То есть, если
\(AC=BC,\) то
\(\angle A=\angle B.\)
▶ 2. Биссектриса, проведенная из вершины равнобедренного треугольника к основанию, является медианой и высотой.
Замечание:
1) Если в треугольнике биссектриса совпадает с медианой, то он равнобедренный.
2) Если в треугольнике медиана совпадает с высотой, то он равнобедренный.
3) Если в треугольнике высота совпадает с биссектрисой, то он равнобедренный.
Замечание: Если углы при основании равны, то треугольник равнобедренный.
▶ 3. В равнобедренном треугольнике высоты, медианы и биссектрисы, проведённые из вершин основания, равны.
Замечание: Верны и обратные утверждения:
1) Если в треугольнике две медианы равны, то треугольник равнобедренный.
2) Если в треугольнике две высоты равны, то треугольник равнобедренный.
3) Если в треугольнике две биссектрисы равны, то треугольник равнобедренный.
Первые два утверждения очевидны, а третье не имеет простого доказательства и называется теоремой Штейнера-Лемуса.
Равнобедренный треугольник - это треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона - основанием.





⚡️ посмотри курс изнутри
⚡️ забери задания и методички
⚡️ получи четкий план подготовки
⚡️ пообщайся с экспертами ЕГЭ












